题目内容
16．在下图中，每个图案均由边长为1的小正方形按一定的规律堆叠而成，照此规律，第n个图案中共有n2个小正方形．
分析 观察图案不难发现，图案中的正方形按照从上到下成奇数列排布，写出第n个图案的正方形的个数，然后利用求和公式写出表达式．
解答 解：第1个图案中共有1个小正方形，
第2个图案中共有1+3=4个小正方形，
第3个图案中共有1+3+5=9个小正方形，
…，
第n个图案中共有1+3+5+…+（2n-1）=$\frac{1}{2}$n（1+2n-1）=n2个小正方形．
故答案为：n2．
点评 本题是对图形变化规律的考查，根据图案从上到下的正方形的个数成奇数列排布，得到第n个图案的正方形的个数的表达式是解题的关键．
练习册系列答案
相关题目
如图，在△ABC中，∠ABC=90°，D为AB延长线上一点，点E在BC边上且BE=BD，连结AE、DE、DC，AE=DC．
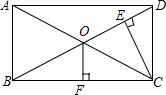如图，从矩形ABCD的一个顶点C向对角线BD作垂线CE，垂足是E，若BE=3DE，两对角线的交点O至BC的距离OF=36cm，求AC的长．
如图，是我国体育健儿在最近六届奥运会上获得奖牌的情况，那么我国体育健儿在这六届奥运会上共获得的奖牌数为286枚．