题目内容
19.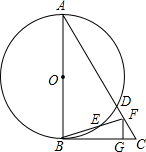 如图,以△ABC边AB为直径的⊙O交AC于点D,点F在DC上,BF交⊙O于点E,BE=EF,∠BAC=2∠CBF,CG⊥BF于点G.
如图,以△ABC边AB为直径的⊙O交AC于点D,点F在DC上,BF交⊙O于点E,BE=EF,∠BAC=2∠CBF,CG⊥BF于点G.(1)求证:BC是⊙O的切线;
(2)若∠C=60°,GC=2,求⊙O的半径.
分析 (1)连接AE,根据圆周角定理求得∠AEB=90°,然后根据垂直平分线的性质求得AB=AF,根据等腰三角形三线合一的性质求得∠BAE=∠FAE=$\frac{1}{2}$∠BAC,从而求得∠BAE=∠FAE=$\frac{1}{2}$∠BAC,即可求得∠BAE+∠ABF=∠CBF+∠ABF=90°,即可证得结论;
(2)根据已知求得CF=4,设AB=AF=x,z则AC=x+4,通过∠C的正弦函数即可求得AB,继而求得⊙O的半径.
解答  (1)证明:连接AE,
(1)证明:连接AE,
∵AB是直径,
∴∠AEB=90°,
∵BE=EF,
∴AB=AF,
∴∠BAE=∠FAE=$\frac{1}{2}$∠BAC,
∵∠BAC=2∠CBF,
∴∠BAE=∠CBF,
∴∠BAE+∠ABF=∠CBF+∠ABF=90°,
即∠ABC=90°,
∴BC是⊙O的切线;
(2)解:∵FG⊥BC,∠C=60°,
∴∠CFG=30°,
∴CF=2CG=4,
∵AF=AB,
设AB=AF=x,z则AC=x+4,
∵∠C=60°,
∴sin∠C=$\frac{AB}{AC}$,
∴$\frac{\sqrt{3}}{2}$=$\frac{x}{x+4}$,解得x=8$\sqrt{3}$+12,
∴AB=8$\sqrt{3}$+12,
∴⊙O的半径为(4$\sqrt{3}$+6).
点评 本题考查了圆周角定理,等腰三角形的判定和性质,切线的判定,直角三角函数等,作出辅助线构建直角三角形是解题的关键.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
9.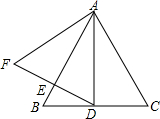 如图,等腰三角形ABC中,AB=AC,∠BAC=70°,D是BC中点,DE⊥AB于E,延长DE至F,使EF=DE,则∠F的度数是( )
如图,等腰三角形ABC中,AB=AC,∠BAC=70°,D是BC中点,DE⊥AB于E,延长DE至F,使EF=DE,则∠F的度数是( )
 如图,等腰三角形ABC中,AB=AC,∠BAC=70°,D是BC中点,DE⊥AB于E,延长DE至F,使EF=DE,则∠F的度数是( )
如图,等腰三角形ABC中,AB=AC,∠BAC=70°,D是BC中点,DE⊥AB于E,延长DE至F,使EF=DE,则∠F的度数是( )| A. | 30° | B. | 35° | C. | 55° | D. | 60° |
10.-(-3)的相反数的倒数是( )
| A. | -$\frac{1}{3}$ | B. | 3 | C. | $\frac{1}{3}$ | D. | -3 |
14.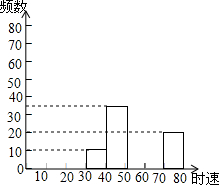 小明将我市交通部门在某雷达测速区监测到的一组汽车的时速数据进行收集、整理,制作成如下不完整的统计图表,根据提供的信息解答下列问题:
小明将我市交通部门在某雷达测速区监测到的一组汽车的时速数据进行收集、整理,制作成如下不完整的统计图表,根据提供的信息解答下列问题:
(1)把表中的数据填写完整;
(2)补全频数分布直方图;
(3)如果汽车时速大于或等于60千米即为违章,则违章车辆共有多少辆?
 小明将我市交通部门在某雷达测速区监测到的一组汽车的时速数据进行收集、整理,制作成如下不完整的统计图表,根据提供的信息解答下列问题:
小明将我市交通部门在某雷达测速区监测到的一组汽车的时速数据进行收集、整理,制作成如下不完整的统计图表,根据提供的信息解答下列问题:(1)把表中的数据填写完整;
(2)补全频数分布直方图;
(3)如果汽车时速大于或等于60千米即为违章,则违章车辆共有多少辆?
| 时速x(km/h) | 频 数 | 频 率 |
| 30≤x≤40 | 10 | 0.05 |
| 40≤x≤50 | 36 | 0.18 |
| 50≤x≤60 | 78 | 0.39 |
| 60≤x≤70 | 56 | 0.28 |
| 70≤x≤80 | 20 | 0.10 |
| 总 计 | 200 | 1 |
9.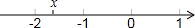 实数x在数轴上位置如图,则x0,x-1,x-2,x-4的大小关系为( )
实数x在数轴上位置如图,则x0,x-1,x-2,x-4的大小关系为( )
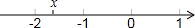 实数x在数轴上位置如图,则x0,x-1,x-2,x-4的大小关系为( )
实数x在数轴上位置如图,则x0,x-1,x-2,x-4的大小关系为( )| A. | x0>x-1>x-2>x-4 | B. | x-4>x-2>x-1>x0 | C. | x-2>x-4>x0>x-1 | D. | x0>x-2>x-4>x-1 |
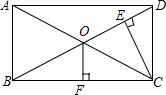 如图,从矩形ABCD的一个顶点C向对角线BD作垂线CE,垂足是E,若BE=3DE,两对角线的交点O至BC的距离OF=36cm,求AC的长.
如图,从矩形ABCD的一个顶点C向对角线BD作垂线CE,垂足是E,若BE=3DE,两对角线的交点O至BC的距离OF=36cm,求AC的长.