题目内容
若关于x的一元二次方程x2-4x+1-t=0（t为实数），在-1＜x＜
的范围内有解，则t的取值范围是 ．
| 7 |
| 2 |
考点：抛物线与x轴的交点
专题：
分析：因为方程在-1和
这两个地方的函数值，必然是异号的，这样才能保证函数在-1＜x＜
之间与x轴相交，方程才有解，进而求出t的取值范围．
| 7 |
| 2 |
| 7 |
| 2 |
解答：解：设y=x2-4x+1-t；
∵-1＜x＜
，
∴△=16-4（1-t）=12+4t≥0，
t≥-3；
∵对称轴为x=2，
∴x=-1时，y=1+4+1-t＞0，
解得：t＜6；
所以-1≤t＜6，
故答案为：-3≤t＜6．
∵-1＜x＜
| 7 |
| 2 |
∴△=16-4（1-t）=12+4t≥0，
t≥-3；
∵对称轴为x=2，
∴x=-1时，y=1+4+1-t＞0，
解得：t＜6；
所以-1≤t＜6，
故答案为：-3≤t＜6．
点评：本题考查了一元二次方程根的分布问题，必须结合函数来做的，一元二次方程和函数本来就是紧密相连的，必须要掌握．
练习册系列答案
相关题目
△ABC中，D是BC的中点．分别以AB，AC为一边，向三角形内部作Rt△ABE，Rt△ACF，使∠ABE=∠ACF，连接DE，DF，求证：DE=DF．
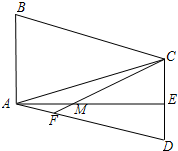已知：在?ABCD中，AE⊥CD，垂足为E，点M为AE上一点，且ME=AB，AM=CE，连接CM并延长交AD于点F．
如图，AB是⊙O的弦，OP⊥AB交⊙O于C，OC=2，∠ABC=30°．
如图，以等腰直角△ABC两锐角顶点A、B为圆心作等圆，⊙A与⊙B恰好外切，若AC=2，那么图中两个扇形（即阴影部分）的面积之和为
如图，圆盘被分成8个全等的小扇形，分别涂上红、黄、白3种颜色．如果小明将飞镖随意投中圆盘，投中白色扇形的概率是