题目内容
已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M,N.
(1)当∠MAN绕点A旋转到BM≠DN时(图2),线段BM,DN和MN之间有怎样的数量关系?写出猜想,并加以证明.
(2)当∠MAN绕点A旋转到(图3)的位置时,线段BM,DN和MN之间又有怎样的数量关系?证明你的猜想.
(3)若正方形的边长为4,当点N运动到DC边的中点处时,求BM的长.

(1)当∠MAN绕点A旋转到BM≠DN时(图2),线段BM,DN和MN之间有怎样的数量关系?写出猜想,并加以证明.
(2)当∠MAN绕点A旋转到(图3)的位置时,线段BM,DN和MN之间又有怎样的数量关系?证明你的猜想.
(3)若正方形的边长为4,当点N运动到DC边的中点处时,求BM的长.

考点:旋转的性质,全等三角形的判定与性质,正方形的性质
专题:
分析:(1)BM+DN=MN成立,证得B、E、M三点共线即可得到△AEM≌△ANM,从而证得ME=MN;
(2)DN-BM=MN.证明方法与(1)类似;
(3)根据(1)可知,BM+DN=MN,设 MN=x,则 BM=x-2,则CM=4-(x-2)=6-x,在Rt△CMN中,利用MN2=CM2+CN2,求出即可.
(2)DN-BM=MN.证明方法与(1)类似;
(3)根据(1)可知,BM+DN=MN,设 MN=x,则 BM=x-2,则CM=4-(x-2)=6-x,在Rt△CMN中,利用MN2=CM2+CN2,求出即可.
解答: 解:(1)BM+DN=MN成立.
解:(1)BM+DN=MN成立.
理由:如图2,把△ADN绕点A顺时针旋转90°,
得到△ABE,则可证得E、B、M三点共线(图形画正确).
∴∠EAM=90°-∠NAM=90°-45°=45°,
又∵∠NAM=45°,
在△AEM与△ANM中,
∴△AEM≌△ANM(SAS),
∴ME=MN,
∵ME=BE+BM=DN+BM,
∴DN+BM=MN;
(2)DN-BM=MN.
理由:如图3,在线段DN上截取DQ=BM,
在△AMN和△AQN中,
∴△AMN≌△AQN(SAS),
∴MN=QN,
∴DN-BM=MN.
(3)如图1,
∵正方形的边长为4,DN=2,
∴CN=2.
根据(1)可知,BM+DN=MN,
设 MN=x,则 BM=x-2,
∴CM=4-(x-2)=6-x.
在Rt△CMN中,
∵MN2=CM2+CN2,
∴x2=(6-x)2+22.
解得 x=
.
∴MB=
-2=
.
 解:(1)BM+DN=MN成立.
解:(1)BM+DN=MN成立.理由:如图2,把△ADN绕点A顺时针旋转90°,
得到△ABE,则可证得E、B、M三点共线(图形画正确).
∴∠EAM=90°-∠NAM=90°-45°=45°,
又∵∠NAM=45°,
在△AEM与△ANM中,
|
∴△AEM≌△ANM(SAS),
∴ME=MN,
∵ME=BE+BM=DN+BM,

∴DN+BM=MN;
(2)DN-BM=MN.
理由:如图3,在线段DN上截取DQ=BM,
在△AMN和△AQN中,
|
∴△AMN≌△AQN(SAS),
∴MN=QN,
∴DN-BM=MN.
(3)如图1,
∵正方形的边长为4,DN=2,
∴CN=2.
根据(1)可知,BM+DN=MN,
设 MN=x,则 BM=x-2,
∴CM=4-(x-2)=6-x.
在Rt△CMN中,
∵MN2=CM2+CN2,
∴x2=(6-x)2+22.
解得 x=
| 10 |
| 3 |
∴MB=
| 10 |
| 3 |
| 4 |
| 3 |
点评:此题考查正方形的性质、全等三角形的判定和性质、勾股定理等知识点,运用截长补短法构造全等三角形是关键.也可运用图形的旋转性质构造全等三角形.

练习册系列答案
相关题目
甲、乙两个芭蕾舞团女演员的平均身高是
甲=165,
乙=165,她们身高的方差是S甲2=1.5,S乙2=2.5.下列说法正确的是( )
. |
| x |
. |
| x |
| A、甲团演员身高更整齐 |
| B、乙团演员身高更整齐 |
| C、两团演员身高一样更整齐 |
| D、无法确定谁更整齐 |
 如图,直线y=-
如图,直线y=-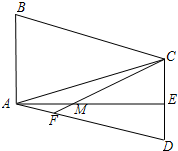 已知:在?ABCD中,AE⊥CD,垂足为E,点M为AE上一点,且ME=AB,AM=CE,连接CM并延长交AD于点F.
已知:在?ABCD中,AE⊥CD,垂足为E,点M为AE上一点,且ME=AB,AM=CE,连接CM并延长交AD于点F.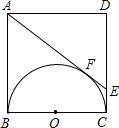 在边长为a的正方形内ABCD中,AE与以BC为直径的半圆相切于点F,交CD于E,求CF、FD的长.
在边长为a的正方形内ABCD中,AE与以BC为直径的半圆相切于点F,交CD于E,求CF、FD的长. 如图,以等腰直角△ABC两锐角顶点A、B为圆心作等圆,⊙A与⊙B恰好外切,若AC=2,那么图中两个扇形(即阴影部分)的面积之和为
如图,以等腰直角△ABC两锐角顶点A、B为圆心作等圆,⊙A与⊙B恰好外切,若AC=2,那么图中两个扇形(即阴影部分)的面积之和为 如图,在四边形ABCD中,AD∥BC,∠BCD=90°,∠ABC=45°,AD=CD,CE平分∠ACB交AB于点E,在BC上截取BF=AE,连接AF交CE于点G,连接DG交AC于点H,过点A作AN⊥BC,垂足为N,AN交CE于点M.则下列结论:
如图,在四边形ABCD中,AD∥BC,∠BCD=90°,∠ABC=45°,AD=CD,CE平分∠ACB交AB于点E,在BC上截取BF=AE,连接AF交CE于点G,连接DG交AC于点H,过点A作AN⊥BC,垂足为N,AN交CE于点M.则下列结论: