题目内容
抛物线y=-3x2-x+4与坐标轴的交点个数是 ．
考点：抛物线与x轴的交点
专题：
分析：根据抛物线与x轴交点个数由b2-4ac符号进而得出答案，再利用抛物线开口方向得出图象与y轴有一个交点，即可得出答案．
解答：解：∵y=-3x2-x+4，
∴b2-4ac=（-1）2-4×（-3）×4=49＞0，
∴抛物线与x轴有两个交点，
∵a=-3＜0，
∴抛物线与y轴有一个交点，
∴抛物线y=-3x2-x+4与坐标轴的交点个数是3．
故答案为：3．
∴b2-4ac=（-1）2-4×（-3）×4=49＞0，
∴抛物线与x轴有两个交点，
∵a=-3＜0，
∴抛物线与y轴有一个交点，
∴抛物线y=-3x2-x+4与坐标轴的交点个数是3．
故答案为：3．
点评：此题主要考查了抛物线与x轴交点个数确定方法，得出b2-4ac符号是解题关键．
练习册系列答案
相关题目
已知：在?ABCD中，AE⊥CD，垂足为E，点M为AE上一点，且ME=AB，AM=CE，连接CM并延长交AD于点F．
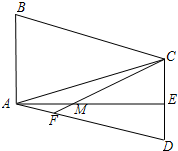
如图，以等腰直角△ABC两锐角顶点A、B为圆心作等圆，⊙A与⊙B恰好外切，若AC=2，那么图中两个扇形（即阴影部分）的面积之和为
如图，在四边形ABCD中，AD∥BC，∠BCD=90°，∠ABC=45°，AD=CD，CE平分∠ACB交AB于点E，在BC上截取BF=AE，连接AF交CE于点G，连接DG交AC于点H，过点A作AN⊥BC，垂足为N，AN交CE于点M．则下列结论：
如图，圆盘被分成8个全等的小扇形，分别涂上红、黄、白3种颜色．如果小明将飞镖随意投中圆盘，投中白色扇形的概率是
如图，直角三角形ABO放置在平面直角坐标系中，已知斜边OA在x轴正半轴上，且OA=4，AB=2，将该三角形绕着点O逆时针旋转120°后点B的对应点恰好落在一反比例函数图象上，则该反比例函数的解析式为