题目内容
4. 如图,在长方形ABCD中,AB>BC,BE⊥AC,垂足为E,延长BE交CD于F,S表示面积,则给出的下列命题:
如图,在长方形ABCD中,AB>BC,BE⊥AC,垂足为E,延长BE交CD于F,S表示面积,则给出的下列命题:①Rt△ABC≌Rt△CDA;②S△AEF<S△BCE;③∠DAE+∠DFE=180°;④∠AFB>∠ACB
其中正确命题的代号是①③④.
分析 由矩形的性质得出∠ABC=∠D=∠BCD=∠BAD=90°,BC=DA,AB=CD,由SAS证明△ABC≌△CDA,①正确;
由△ABF的面积=△ABC的面积,得出△AEF的面积=△BCE的面积,②不正确;
证明A、E、F、D四点共圆,得出∠DAE+∠DFE=180°,③正确;
延长AF交矩形ABCD的外接圆于G,连接BG,由圆周角定理得出∠AGB=∠ACB,由三角形的外角性质得出∠AFB>∠AGB,得出∠AFB>∠ACB,④正确;即可得出结论.
解答 解:∵四边形ABCD是矩形,
∴∠ABC=∠D=∠BCD=∠BAD=90°,BC=DA,AB=CD,
在△ABC和△CDA中,$\left\{\begin{array}{l}{AB=CD}&{\;}\\{∠ABC=∠D}&{\;}\\{BC=DA}&{\;}\end{array}\right.$,
∴△ABC≌△CDA(SAS),
∴①正确;
∵△ABF的面积=△ABC的面积=AB•BC,
∴△AEF的面积=△BCE的面积,
∴②不正确;
∵BE⊥AC,
∴∠AEF=90°,
∴∠AEF+∠D=180°,
∴A、E、F、D四点共圆,
∴∠DAE+∠DFE=180°,
∴③正确;
∵A、B、C、D四点共圆,
如图所示: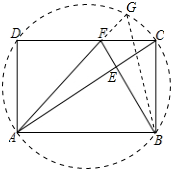 延长AF交矩形ABCD的外接圆于G,连接BG,
延长AF交矩形ABCD的外接圆于G,连接BG,
则∠AGB=∠ACB,
∵∠AFB>∠AGB,
∴∠AFB>∠ACB,
∴④正确;
正确的代号是①③④;
故答案为:①③④.
点评 本题考查了矩形的性质、全等三角形的判定与性质、四点共圆、圆周角定理、圆内接四边形的性质;熟练掌握矩形的性质,并能进行推理论证是解决问题的关键.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
15.已知a>b,下列四个不等式中不正确的是( )
| A. | 4a>4b | B. | -4a<-4b | C. | a+4>b+4 | D. | a-4<b-4 |
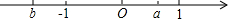 实数a、b在数轴上的位置如图所示,写出不等式组$\left\{\begin{array}{l}x+a>0\\ x-b>0\end{array}$的解集为x>-a.
实数a、b在数轴上的位置如图所示,写出不等式组$\left\{\begin{array}{l}x+a>0\\ x-b>0\end{array}$的解集为x>-a.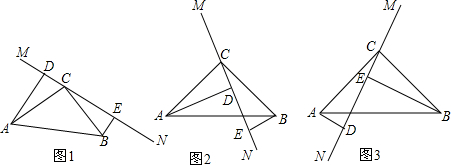
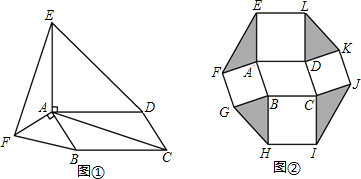
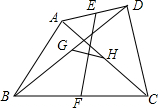 如图,在四边形ABCD中,E、F分别是AD、BC的中点,G、H分别是BD、AC的中点,当AB、CD满足条件AB=CD时,有EF⊥GH.
如图,在四边形ABCD中,E、F分别是AD、BC的中点,G、H分别是BD、AC的中点,当AB、CD满足条件AB=CD时,有EF⊥GH.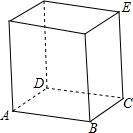 如图是一个长方体,AB=x,BC=$\frac{6}{5}$x,CE=10,则长方体的体积y与x之间的函数解析式是y=12x2,y是x的二次函数.
如图是一个长方体,AB=x,BC=$\frac{6}{5}$x,CE=10,则长方体的体积y与x之间的函数解析式是y=12x2,y是x的二次函数.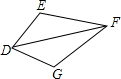 填空:如图,请你选择合适的条件填入空格中,使两个三角形全等.
填空:如图,请你选择合适的条件填入空格中,使两个三角形全等.