题目内容
9.在现实生活中,我们经常会看到许多“标准”的矩形,如我们的课本封面、A4的打印纸等,其实这些矩形的长与宽之比都为$\sqrt{2}$:1,我们不妨就把这样的矩形称为“标准矩形”,在“标准矩形”ABCD中,P为DC边上一定点,且CP=BC,如图所示.
(1)如图①,求证:BA=BP;
(2)如图②,点Q在DC上,且DQ=CP,若G为BC边上一动点,当△AGQ的周长最小时,求$\frac{CG}{GB}$的值;
(3)如图③,已知AD=1,在(2)的条件下,连接AG并延长交DC的延长线于点F,连接BF,T为BF的中点,M、N分别为线段PF与AB上的动点,且始终保持PM=BN,请证明:△MNT的面积S为定值,并求出这个定值.
分析 (1)如图①中,设AD=BC=a,则AB=CD=$\sqrt{2}$a.通过计算得出AB=BP=$\sqrt{2}$a,由此即可证明;
(2)如图②中,作Q关于BC的对称点Q′,连接AQ′交BC于G,此时△AQG的周长最小.设AD=BC=QD=a,则AB=CD=$\sqrt{2}$a,可得CQ=CQ′=$\sqrt{2}$a-a,由CQ′∥AB,推出$\frac{CG}{GB}$=$\frac{CQ′}{AB}$=$\frac{\sqrt{2}a-a}{\sqrt{2}a}$=$\frac{2-\sqrt{2}}{2}$;
(3)如图③中,作TH∥AB交NM于H,交BC于K.由S△MNT=$\frac{1}{2}$•TH•CK+$\frac{1}{2}$•TH•BK=$\frac{1}{2}$HT•(KC+KB)=$\frac{1}{2}$HT•BC=$\frac{1}{2}$HT,利用梯形的中位线定理求出HT即可解决问题;
解答 (1)证明:如图①中,设AD=BC=a,则AB=CD=$\sqrt{2}$a.
∵四边形ABCD是矩形,
∴∠C=90°,
∵PC=AD=BC=a,
∴PB=$\sqrt{P{C}^{2}+B{C}^{2}}$=$\sqrt{2}$a,
∴BA=BP.
(2)解:如图②中,作Q关于BC的对称点Q′,连接AQ′交BC于G,此时△AQG的周长最小.
设AD=BC=QD=a,则AB=CD=$\sqrt{2}$a,
∴CQ=CQ′=$\sqrt{2}$a-a,
∵CQ′∥AB,
∴$\frac{CG}{GB}$=$\frac{CQ′}{AB}$=$\frac{\sqrt{2}a-a}{\sqrt{2}a}$=$\frac{2-\sqrt{2}}{2}$.
(3)证明:如图③中,作TH∥AB交NM于H,交BC于K.
由(2)可知,AD=BC=1,AB=CD=$\sqrt{2}$,DP=CF=$\sqrt{2}$-1,
∵S△MNT=$\frac{1}{2}$•TH•CK+$\frac{1}{2}$•TH•BK=$\frac{1}{2}$HT•(KC+KB)=$\frac{1}{2}$HT•BC=$\frac{1}{2}$HT,
∵TH∥AB∥FM,TF=TB,
∴HM=HN,
∴HT=$\frac{1}{2}$(FM+BN),
∵BN=PM,
∴HT=$\frac{1}{2}$(FM+PM)=$\frac{1}{2}$PF=$\frac{1}{2}$•(1+$\sqrt{2}$-1)=$\frac{\sqrt{2}}{2}$,
∴S△MNT=$\frac{1}{2}$HT=$\frac{\sqrt{2}}{4}$=定值.
点评 本题考查相似形综合题、矩形的性质、平行线分线段成比例定理、勾股定理、梯形的中位线定理等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,构造梯形的中位线解决问题,属于中考压轴题.

 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案 如图,四边形ABCD内接于⊙O,DA=DC,∠CBE=50°,则∠DAC的大小为( )
如图,四边形ABCD内接于⊙O,DA=DC,∠CBE=50°,则∠DAC的大小为( )| A. | 130° | B. | 100° | C. | 65° | D. | 50° |
| A. |  | B. |  | C. |  | D. |  |
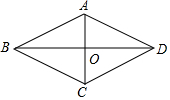 求证:菱形的两条对角线互相垂直.
求证:菱形的两条对角线互相垂直.已知:如图,四边形ABCD是菱形,对角线AC,BD交于点O.
求证:AC⊥BD.
以下是排乱的证明过程:
①又BO=DO;
②∴AO⊥BD,即AC⊥BD;
③∵四边形ABCD是菱形;
④∴AB=AD.
证明步骤正确的顺序是( )
| A. | ③→②→①→④ | B. | ③→④→①→② | C. | ①→②→④→③ | D. | ①→④→③→② |

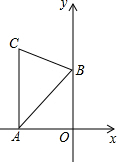 如图,AC⊥x轴于点A,点B在y轴的正半轴上,∠ABC=60°,AB=4,BC=2$\sqrt{3}$,点D为AC与反比例函数y=$\frac{k}{x}$的图象的交点.若直线BD将△ABC的面积分成1:2的两部分,则k的值为-4或-8.
如图,AC⊥x轴于点A,点B在y轴的正半轴上,∠ABC=60°,AB=4,BC=2$\sqrt{3}$,点D为AC与反比例函数y=$\frac{k}{x}$的图象的交点.若直线BD将△ABC的面积分成1:2的两部分,则k的值为-4或-8.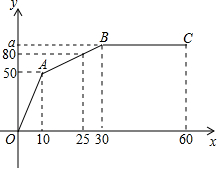 “和谐号”火车从车站出发,在行驶过程中速度y(单位:m/s)与时间x(单位:s)的关系如图所示,其中线段BC∥x轴.
“和谐号”火车从车站出发,在行驶过程中速度y(单位:m/s)与时间x(单位:s)的关系如图所示,其中线段BC∥x轴.