题目内容
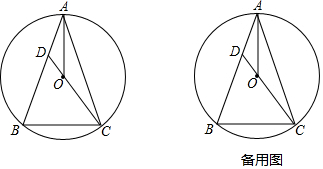
17．
如图，四边形ABCD内接于⊙O，DA=DC，∠CBE=50°，则∠DAC的大小为（ ）| A． | 130° | B． | 100° | C． | 65° | D． | 50° |
分析 先根据补角的性质求出∠ABC的度数，再由圆内接四边形的性质求出∠ADC的度数，由等腰三角形的性质求得∠DAC的度数．
解答 解：∵∠CBE=50°，
∴∠ABC=180°-∠CBE=180°-50°=130°，
∵四边形ABCD为⊙O的内接四边形，
∴∠D=180°-∠ABC=180°-130°=50°，
∵DA=DC，
∴∠DAC=$\frac{180°-∠D}{2}$=65°，
故选C．
点评 本题考查的是圆内接四边形的性质及等腰三角形的性质，即在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．
练习册系列答案
相关题目
国家推行“节能减排，低碳经济”政策后，某环保节能设备生产的产品供不应求，若该企业的某种环保设备每月的产量保持在一定的范围，每套产品的生产成本不高于44万元，每套产品的售价不低于80万元．已知这种设备的月产量x（套）与每套的售价y1（万元）间满足关系式y1=160-2x，月产量x（套）与生产总成本y2（万元）存在如图所示的函数关系．
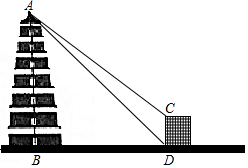“大雁塔”是西安市的标志性建筑、著名古迹、唐代永徽三年，玄樊为藏经典而修建，塔身七层，被视为古都西安的象征．民间人士道：“不到大雁塔，不算到西安”．小明在学习了锐角三角函数后，想用所学知识测量“大雁塔”的高度，小明在一栋高15米的建筑物底部D处侧得塔顶端A的仰角为45°，接着在建筑物顶端C处测得塔顶端A的仰角为37.5°．已知AB⊥BD，CD⊥BD，请你根据题中提供的相关信息，求出“大雁塔”的高AB的长度．（结果精确到0.1米）（参考数据：sin37.5°≈0.6088，cos37.5°≈0.7934，tan37.5°≈0.7673．
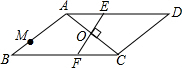如图，在?ABCD中，∠B=30°，AB=AC，O是两条对角线的交点，过点O作AC的垂线分别交边AD，BC于点E，F；点M是边AB的一个三等分点，则△AOE与△BMF的面积比为3：4．
