题目内容
19. 如图,点C在以AB为直径的半圆⊙O上,BE,AD分别为∠ABC,∠CAB的角平分线,AB=6,则DE的长为( )
如图,点C在以AB为直径的半圆⊙O上,BE,AD分别为∠ABC,∠CAB的角平分线,AB=6,则DE的长为( )| A. | 3 | B. | 3$\sqrt{2}$ | C. | 3$\sqrt{3}$ | D. | 5 |
分析 连结OE,OD.先证明∠CAB+∠CBA=90°,由角平分线的定义可证明∠DAB+∠EBA=45°,接下来,利用圆周角定理可知可证明∠AOE+∠BOD=90°,则△EOD为等腰直角三角形,最后利用特殊锐角三角函数值可求得ED的长.
解答 解:连结OE,OD.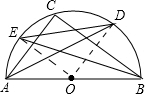
∵AB为⊙O的直径,
∴∠ACB=90°.
∴∠CAB+∠CBA=90°.
∵BE,AD分别为∠ABC,∠CAB的角平分线,
∴∠DAB+∠EBA=45°.
由圆周角定理可知∠AOE=2∠ABE,∠DOB=2∠DAB,
∴∠AOE+∠BOD=90°.
∴∠EOD=90°.
∵AB=6,
∴OE=OD=3.
∴ED=$\sqrt{2}$OE=3$\sqrt{2}$.
故选:B.
点评 本题主要考查的是圆周角定理以及其推理的应用、特殊锐角三角函数值,得到△EOD为等腰直角三角形是解题的关键.

练习册系列答案
相关题目
9. 一个商标图案如图4中阴影部分,在长方形ABCD中,AB=6cm,BC=4cm,以点A为圆心,AD为半径作圆与BA的延长线相交于点F,则阴影部分的面积是( )
一个商标图案如图4中阴影部分,在长方形ABCD中,AB=6cm,BC=4cm,以点A为圆心,AD为半径作圆与BA的延长线相交于点F,则阴影部分的面积是( )
 一个商标图案如图4中阴影部分,在长方形ABCD中,AB=6cm,BC=4cm,以点A为圆心,AD为半径作圆与BA的延长线相交于点F,则阴影部分的面积是( )
一个商标图案如图4中阴影部分,在长方形ABCD中,AB=6cm,BC=4cm,以点A为圆心,AD为半径作圆与BA的延长线相交于点F,则阴影部分的面积是( )| A. | (4π+4)cm2 | B. | (4π+8)cm2 | C. | (8π+4)cm2 | D. | (4π-16)cm2 |
10.一位同学用三根木棒拼成如下图形,则其中符合三角形概念的是( )
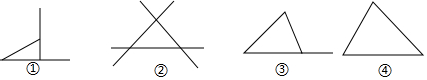
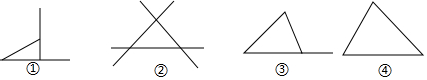
| A. | ① | B. | ② | C. | ③ | D. | ④ |
7.用直尺和圆规作一个角等于已知角,如图,能得出∠A′O′B′=∠AOB的依据是( )


| A. | SAS | B. | AAS | C. | ASA | D. | SSS |
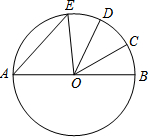 如图,AB是⊙O的直径,$\widehat{BC}$=$\widehat{CD}$=$\widehat{DE}$,∠COD=34°,则∠AEO的度数是51°.
如图,AB是⊙O的直径,$\widehat{BC}$=$\widehat{CD}$=$\widehat{DE}$,∠COD=34°,则∠AEO的度数是51°. 如图,在平面直角坐标系中,二次函数y=ax2+bx+6的图象交x轴于A、B两点,交y轴于点D,点C为抛物线的顶点,且A、B两点的横坐标分别为1和3.
如图,在平面直角坐标系中,二次函数y=ax2+bx+6的图象交x轴于A、B两点,交y轴于点D,点C为抛物线的顶点,且A、B两点的横坐标分别为1和3. 如图,抛物线顶点坐标为点C(2,8),交x轴于点A(6,0),交y轴于点B.
如图,抛物线顶点坐标为点C(2,8),交x轴于点A(6,0),交y轴于点B. 如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.
如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.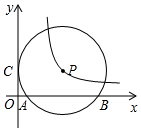 如图,⊙P与y轴相切于点C(0,3),与x轴相交于点A(1,0),B(9,0).双曲线y=$\frac{k}{x}$恰好经过圆心P,那么k的值是15.
如图,⊙P与y轴相切于点C(0,3),与x轴相交于点A(1,0),B(9,0).双曲线y=$\frac{k}{x}$恰好经过圆心P,那么k的值是15.