Question

14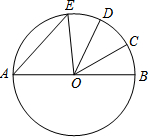．如图，AB是⊙O的直径，$\widehat{BC}$=$\widehat{CD}$=$\widehat{DE}$，∠COD=34°，则∠AEO的度数是51°．

Answer 1

分析 由$\widehat{BC}$=$\widehat{CD}$=$\widehat{DE}$，可求得∠BOC=∠EOD=∠COD=34°，继而可求得∠AOE的度数；然后再根据等腰三角形的性质和三角形内角和定理来求∠AEO的度数．

解答 解：如图，∵$\widehat{BC}$=$\widehat{CD}$=$\widehat{DE}$，∠COD=34°，
∴∠BOC=∠EOD=∠COD=34°，
∴∠AOE=180°-∠EOD-∠COD-∠BOC=78°．
又∵OA=OE，
∴∠AEO=∠OAE，
∴∠AEO=$\frac{1}{2}$×（180°-78°）=51°．
故答案为：51°．

点评 此题考查了弧与圆心角的关系．此题比较简单，注意掌握数形结合思想的应用．