题目内容
10.在矩形ABCD中,AB=4,BC=10,点E为AD上一点(不与A、D重合),当△BCE为直角三角形时AE=2或8.分析 根据勾股定理和矩形的性质解答即可.
解答 解:如图:
设AE为x,
在Rt△ABE中,可得:AB2+AE2=BE2,即42+x2=BE2,
在Rt△CDE中,可得:CD2+DE2=CE2,即42+(10-x)2=CE2,
在Rt△BEC中,可得:BE2+EC2=BC2,即42+x2+42+(10-x)2=102,
解得:x=2或x=8,
答:当△BCE为直角三角形时AE=2或8,
故答案为:2或8.
点评 此题考查矩形的性质,关键是根据勾股定理列出方程解答.

练习册系列答案
相关题目
4. 如图,四边形ABCD中,AB=AC=AD,E是BC的中点,AE=CE,∠BAC=3∠CBD,BD=6$\sqrt{2}$+6$\sqrt{6}$,则AB的长为( )
如图,四边形ABCD中,AB=AC=AD,E是BC的中点,AE=CE,∠BAC=3∠CBD,BD=6$\sqrt{2}$+6$\sqrt{6}$,则AB的长为( )
 如图,四边形ABCD中,AB=AC=AD,E是BC的中点,AE=CE,∠BAC=3∠CBD,BD=6$\sqrt{2}$+6$\sqrt{6}$,则AB的长为( )
如图,四边形ABCD中,AB=AC=AD,E是BC的中点,AE=CE,∠BAC=3∠CBD,BD=6$\sqrt{2}$+6$\sqrt{6}$,则AB的长为( )| A. | 6 | B. | 6$\sqrt{2}$ | C. | 12 | D. | 10$\sqrt{2}$ |
11.实数a,b,c满足a2+6b=-17,b2+8c=-23,c2+2a=14,则a+b+c的值是( )
| A. | -6 | B. | -7 | C. | -8 | D. | -9 |
8. 如图所示:∠CAB=∠BCD,AD=2,BD=4,则BC=( )
如图所示:∠CAB=∠BCD,AD=2,BD=4,则BC=( )
 如图所示:∠CAB=∠BCD,AD=2,BD=4,则BC=( )
如图所示:∠CAB=∠BCD,AD=2,BD=4,则BC=( )| A. | $2\sqrt{2}$ | B. | $2\sqrt{6}$ | C. | 3 | D. | 6 |
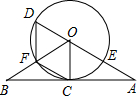 如图,直线AB经过⊙O上的C点,OA、OB分别与⊙O相于E点和F点,且EA=FB,CA=CB,AO的延长线交⊙O于点D.
如图,直线AB经过⊙O上的C点,OA、OB分别与⊙O相于E点和F点,且EA=FB,CA=CB,AO的延长线交⊙O于点D.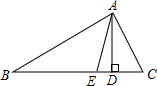 如图所示,已知在△ABC中,AD⊥BC于D,AE平分∠BAC,若∠B=28°,∠DAE=16°,求∠C的度数.
如图所示,已知在△ABC中,AD⊥BC于D,AE平分∠BAC,若∠B=28°,∠DAE=16°,求∠C的度数.