题目内容
3.若函数y=$\frac{1}{2}$(x2-100x+196+|x2-100x+196|),则自变量x取1,2,3,4,…99,100这100个自然数时,函数和的值是( )| A. | 540 | B. | 390 | C. | 194 | D. | 97 |
分析 将x2-100x+196分解为:(x-2)(x-98),然后可得当2≤x≤98时函数值为0,再分别求出x=1,99,100时的函数值即可.
解答 解:∵x2-100x+196=(x-2)(x-98)
∴当2≤x≤98时,|x2-100x+196|=-(x2-100x+196),
当自变量x取2到98时函数值为0,
而当x取1,99,100时,|x2-100x+196|=x2-100x+196,
所以,所求和为(1-2)(1-98)+(99-2)(99-98)+(100-2)(100-98)=97+97+196=390.
故选B.
点评 本题考查函数值的知识,有一定难度,关键是将x2-100x+196分解为:(x-2)(x-98)进行解答.

练习册系列答案
相关题目
11.实数a,b,c满足a2+6b=-17,b2+8c=-23,c2+2a=14,则a+b+c的值是( )
| A. | -6 | B. | -7 | C. | -8 | D. | -9 |
18.下列不等式中,正确的个数是( )
-4$\frac{2}{3}$>-4.7,-$\frac{12}{23}$<-$\frac{6}{11}$,-0.$\stackrel{•}{2}$>-0.22,-0.01<-$\frac{1}{100}$.
-4$\frac{2}{3}$>-4.7,-$\frac{12}{23}$<-$\frac{6}{11}$,-0.$\stackrel{•}{2}$>-0.22,-0.01<-$\frac{1}{100}$.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
8. 如图所示:∠CAB=∠BCD,AD=2,BD=4,则BC=( )
如图所示:∠CAB=∠BCD,AD=2,BD=4,则BC=( )
 如图所示:∠CAB=∠BCD,AD=2,BD=4,则BC=( )
如图所示:∠CAB=∠BCD,AD=2,BD=4,则BC=( )| A. | $2\sqrt{2}$ | B. | $2\sqrt{6}$ | C. | 3 | D. | 6 |
12. 如图,△ABC和△EFC都是等边三角形,AD是△ABC的高,AB=4,若点E在直线AD上运动,连接DF,则在点E运动过程中,线段DF的最小值是( )
如图,△ABC和△EFC都是等边三角形,AD是△ABC的高,AB=4,若点E在直线AD上运动,连接DF,则在点E运动过程中,线段DF的最小值是( )
 如图,△ABC和△EFC都是等边三角形,AD是△ABC的高,AB=4,若点E在直线AD上运动,连接DF,则在点E运动过程中,线段DF的最小值是( )
如图,△ABC和△EFC都是等边三角形,AD是△ABC的高,AB=4,若点E在直线AD上运动,连接DF,则在点E运动过程中,线段DF的最小值是( )| A. | 1 | B. | 2 | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
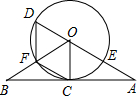 如图,直线AB经过⊙O上的C点,OA、OB分别与⊙O相于E点和F点,且EA=FB,CA=CB,AO的延长线交⊙O于点D.
如图,直线AB经过⊙O上的C点,OA、OB分别与⊙O相于E点和F点,且EA=FB,CA=CB,AO的延长线交⊙O于点D.