题目内容
13. 如图,在?ABCD中,AC,BD交于点O,点E是AB的中点,OE=3cm,则AD的长是6cm.
如图,在?ABCD中,AC,BD交于点O,点E是AB的中点,OE=3cm,则AD的长是6cm.
分析 根据平行四边形的性质可得BO=DO,再根据三角形中位线定理可得AD=2EO,进而可得答案.
解答 解:∵四边形ABCD是平行四边形,
∴BO=DO,
∵点E是AB的中点,
∴EO=$\frac{1}{2}$AD,
∵OE=3,
∴AD=6cm,
故答案为:6.
点评 此题主要考查了平行四边形的性质,以及三角形中位线定理,关键是掌握平行四边形的对角线互相平分.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.若a<-1,则方程x2+(1-2a)x+a2=0根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实根 | ||
| C. | 没有实数根 | D. | 不能确定 |
11.实数a,b,c满足a2+6b=-17,b2+8c=-23,c2+2a=14,则a+b+c的值是( )
| A. | -6 | B. | -7 | C. | -8 | D. | -9 |
12. 如图,△ABC和△EFC都是等边三角形,AD是△ABC的高,AB=4,若点E在直线AD上运动,连接DF,则在点E运动过程中,线段DF的最小值是( )
如图,△ABC和△EFC都是等边三角形,AD是△ABC的高,AB=4,若点E在直线AD上运动,连接DF,则在点E运动过程中,线段DF的最小值是( )
 如图,△ABC和△EFC都是等边三角形,AD是△ABC的高,AB=4,若点E在直线AD上运动,连接DF,则在点E运动过程中,线段DF的最小值是( )
如图,△ABC和△EFC都是等边三角形,AD是△ABC的高,AB=4,若点E在直线AD上运动,连接DF,则在点E运动过程中,线段DF的最小值是( )| A. | 1 | B. | 2 | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
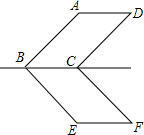 如图,?ABCD与?EBCF关于BC所在直线对称,∠ABE=90°,求∠F.
如图,?ABCD与?EBCF关于BC所在直线对称,∠ABE=90°,求∠F.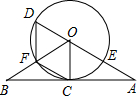 如图,直线AB经过⊙O上的C点,OA、OB分别与⊙O相于E点和F点,且EA=FB,CA=CB,AO的延长线交⊙O于点D.
如图,直线AB经过⊙O上的C点,OA、OB分别与⊙O相于E点和F点,且EA=FB,CA=CB,AO的延长线交⊙O于点D.