题目内容
4.已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.(1)直线BF⊥直线CE于点F,交CD于点G(如图①),求证:AE=CG;
(2)直线BF⊥直线CE于点F,直线AH⊥直线CE于点H,交CD的延长线于点M(如图②),找出图中与BE相等的线段,并证明.
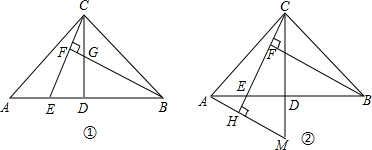
分析 (1)根据题意得到三角形ABC为等腰直角三角形,且CD为斜边上的中线,利用三线合一得到CD垂直于AB,且CD为角平分线,得到∠CAE=∠BCG=45°,再利用同角的余角相等得到一对角相等,AC=BC,利用ASA得到三角形AEC与三角形CGB全等,利用全等三角形的对应边相等即可得证;
(2)由等腰三角形的性质得出∠ACD=∠BCD=∠CBE=45°,利用AAS得到三角形BCE与三角形CAM全等,利用全等三角形的对应边相等即可得证.
解答 (1)证明:∵点D是AB中点,AC=BC,∠ACB=90°,
∴CD⊥AB,∠ACD=∠BCD=45°,
∴∠CAD=∠CBD=45°,
∴∠CAE=∠BCG,
又∵BF⊥CE,
∴∠CBG+∠BCF=90°,
又∵∠ACE+∠BCF=90°,
∴∠ACE=∠CBG,
在△AEC和△CGB中,
$\left\{\begin{array}{l}{∠CAE=∠BCG}&{\;}\\{AC=BC}&{\;}\\{∠ACE=∠CBG}&{\;}\end{array}\right.$,
∴△AEC≌△CGB(ASA),
∴AE=CG;
(2)解:CM=BE;理由如下:
∵AC=BC,∠ACB=90°,点D是AB的中点,
∴CD平分∠ACB,
∴∠ACD=∠BCD=∠CBE=45°,
∵CH⊥HM,CD⊥ED,
∴∠CMA+∠MCH=90°,∠BEC+∠MCH=90°,
∴∠CMA=∠BEC,
在△BCE和△CAM中,
$\left\{\begin{array}{l}{∠CMA=∠BEC}&{\;}\\{∠ACM=∠CBE}&{\;}\\{AC=BC}&{\;}\end{array}\right.$,
∴△BCE≌△CAM(AAS),
∴BE=CM.
点评 此题考查了全等三角形的判定与性质,等腰直角三角形的性质;熟练掌握等腰直角三角形的性质,证明三角形全等三角形是解本题的关键.

| A. | 6 | B. | 8 | C. | 9 | D. | 10 |
| A. | 3y+$\frac{1}{2}x$ | B. | $\frac{x+y}{3}-2y=0$ | C. | y=$\frac{2}{x}+1$ | D. | x2+y=0 |
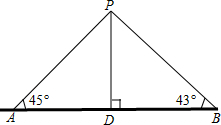 如图,某湖中有一个小岛,湖边有一条笔直的观光小道AB,现决定从小岛建一座与观光小道垂直的小桥PD,测得如下数据:AB=80.0m,∠PAB=45°,∠PBA=43°.求小桥PD的长.(结果精确到0.1m)
如图,某湖中有一个小岛,湖边有一条笔直的观光小道AB,现决定从小岛建一座与观光小道垂直的小桥PD,测得如下数据:AB=80.0m,∠PAB=45°,∠PBA=43°.求小桥PD的长.(结果精确到0.1m)