题目内容
如图所示,一测量员站在岸边的A处,刚好正对河岸另一边B处的一棵大树,这位测量员沿河岸向右走了50 m到达C处,在C处测得∠ACB=38°,求河的宽度.(精确到0.01 m,tan 38°≈0.7813)
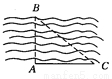
 39.07
【解析】试题分析:在直角三角形中,根据已知条件利用所给角的正切值求得AB即可.
试题解析:在Rt△BAC中,∠ACB=38°.
则AB=AC•tan38°≈50×0.7813=39.065≈39.07(米).
答:河的宽度约为39.07米.
39.07
【解析】试题分析:在直角三角形中,根据已知条件利用所给角的正切值求得AB即可.
试题解析:在Rt△BAC中,∠ACB=38°.
则AB=AC•tan38°≈50×0.7813=39.065≈39.07(米).
答:河的宽度约为39.07米.
练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,求∠ABC的正弦值.
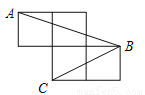
 ∠ABC的正弦值为
【解析】试题分析:首先利用勾股定理计算出AB2,BC2,AC2,再根据勾股定理逆定理可证明∠BCA=90°,然后得到∠ABC的度数,再利用特殊角的三角函数可得∠ABC的正弦值.
试题解析:连接
AB2=32+12=10,BC2=22+12=5,AC=22+12=5,
∴AC=CB,BC2+AC2=AB2,
∴∠BCA=90°,
∴∠ABC=4...
∠ABC的正弦值为
【解析】试题分析:首先利用勾股定理计算出AB2,BC2,AC2,再根据勾股定理逆定理可证明∠BCA=90°,然后得到∠ABC的度数,再利用特殊角的三角函数可得∠ABC的正弦值.
试题解析:连接
AB2=32+12=10,BC2=22+12=5,AC=22+12=5,
∴AC=CB,BC2+AC2=AB2,
∴∠BCA=90°,
∴∠ABC=4... (3分)在Rt△ABC中,∠C=90°,若斜边AB是直角边BC的3倍,则tanB的值是( )
A.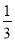 B.3 C.
B.3 C.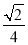 D.
D.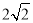
 D.
【解析】
试题分析:设BC=x,则AB=3x,由勾股定理得,AC=,tanB===,故选D.
D.
【解析】
试题分析:设BC=x,则AB=3x,由勾股定理得,AC=,tanB===,故选D. 如图,在△ABC中,BD平分∠ABC,交AC于点D,BC边上有一点E,连接DE,则AD与DE的关系为( )
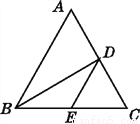
A. AD>DE B. AD=DE
C. AD<DE D. 不确定
 D
【解析】根据角平分线上的点到角的两边距离相等可得点D到AB、BC的距离相等,AD、BE都不是点D到AB、BC的距离,大小不确定.
【解析】
∵BD平分∠ABC,
∴点D到AB、BC的距离相等,
∵AD不是点D到AB的距离,点E是BC上一点,
∴AD、DE的大小不确定.
故选D.
D
【解析】根据角平分线上的点到角的两边距离相等可得点D到AB、BC的距离相等,AD、BE都不是点D到AB、BC的距离,大小不确定.
【解析】
∵BD平分∠ABC,
∴点D到AB、BC的距离相等,
∵AD不是点D到AB的距离,点E是BC上一点,
∴AD、DE的大小不确定.
故选D. 作∠AOB的平分线时,以O为圆心,某一长度为半径作弧,与OA,OB分别相交于点C,D,然后分别以点C,D为圆心,适当的长度为半径作弧,使两弧相交于一点,则这个适当的长度为( )
A. 大于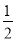 CD B. 等于
CD B. 等于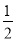 CD
CD
C. 小于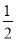 CD D. 以上答案都不对
CD D. 以上答案都不对
 A
【解析】要保证所作的是角平分线,根据全等三角形的性质,则应再保证两弧相交的点到点C、D的距离相等;画弧时,两弧应有交点才能构成三角形,据此结合三角形的三边关系分析即可.
【解析】
根据三角形两边之和大于第三边的性质可知,
画的时候,为了让两条弧有交点,必须是以大于CD的长为半径画弧.
故选A.
A
【解析】要保证所作的是角平分线,根据全等三角形的性质,则应再保证两弧相交的点到点C、D的距离相等;画弧时,两弧应有交点才能构成三角形,据此结合三角形的三边关系分析即可.
【解析】
根据三角形两边之和大于第三边的性质可知,
画的时候,为了让两条弧有交点,必须是以大于CD的长为半径画弧.
故选A. 在Rt△ABC中,BC=3, 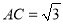 ,
, 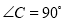 ,则
,则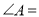 ___________.
___________.
 60°
【解析】试题解析:如图所示:
∵BC=3,AC=,∠C=90°,
∴tanA=,
∴∠A=60°.
故答案为:60°.
60°
【解析】试题解析:如图所示:
∵BC=3,AC=,∠C=90°,
∴tanA=,
∴∠A=60°.
故答案为:60°. 在△ABC中,∠C=90°,a=5,c=17,用科学计算器求∠A约等于 ( )
A. 17.6° B. 17°6′ C. 17°16′ D. 17.16°
 A
【解析】试题解析:sinA=,
A=sin-10.294=17.6°,
故选A.
A
【解析】试题解析:sinA=,
A=sin-10.294=17.6°,
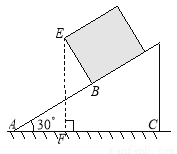
故选A. 一个长方体木箱沿斜面下滑,当木箱滑至如图位置时,AB=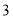 m,已知木箱高BE=
m,已知木箱高BE=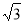 m,斜坡角为30°,则木箱端点E距地面AC的高度EF为 m.
m,斜坡角为30°,则木箱端点E距地面AC的高度EF为 m.
 3.
【解析】
试题分析:连接AE,在Rt△ABE中求出AE,根据∠EAB的正切值求出∠EAB的度数,继而得到∠EAF的度数,在Rt△EAF中,解出EF即可得出答案.
试题解析:连接AE,
在Rt△ABE中,AB=3m,BE=m,
则AE=m,
又∵tan∠EAB=,
∴∠EAB=30°,
在Rt△AEF中,∠EAF=∠EAB+∠BAC=60°,
...
3.
【解析】
试题分析:连接AE,在Rt△ABE中求出AE,根据∠EAB的正切值求出∠EAB的度数,继而得到∠EAF的度数,在Rt△EAF中,解出EF即可得出答案.
试题解析:连接AE,
在Rt△ABE中,AB=3m,BE=m,
则AE=m,
又∵tan∠EAB=,
∴∠EAB=30°,
在Rt△AEF中,∠EAF=∠EAB+∠BAC=60°,
... 用8个除颜色外均相同的球设计一个游戏,使摸到白球与摸不到白球的可能性一样大,摸到红球的可能性比摸到黄球的可能性大,则游戏设计中白、红、黄球的个数可能是( )
A. 4,2,2 B. 3,2,3 C. 4,3,1 D. 5,2,1
 C
【解析】【解析】
∵摸到白球与摸不到白球的可能性一样大,摸到红球的可能性比摸到黄球的可能性大,∴白球4个,红球3个,黄球1个.故选C.
C
【解析】【解析】
∵摸到白球与摸不到白球的可能性一样大,摸到红球的可能性比摸到黄球的可能性大,∴白球4个,红球3个,黄球1个.故选C. 
