题目内容
如图1,Rt△ABC两直角边的边长为AC=3,BC=4.
(1)如图2,⊙O与Rt△ABC的边AB相切于点X,与边BC相切于点Y.请你在图2中作出并标明⊙O的圆心(用尺规作图,保留作图痕迹,不写作法和证明)
(2)P是这个Rt△ABC上和其内部的动点,以P为圆心的⊙P与Rt△ABC的两条边相切.设⊙P的面积为S,你认为能否确定S的最大值?若能,请你求出S的最大值;若不能,请你说明不能确定S的最大值的理由.
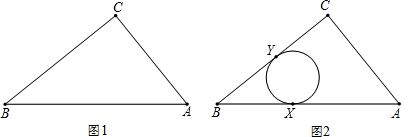
(1)如图2,⊙O与Rt△ABC的边AB相切于点X,与边BC相切于点Y.请你在图2中作出并标明⊙O的圆心(用尺规作图,保留作图痕迹,不写作法和证明)
(2)P是这个Rt△ABC上和其内部的动点,以P为圆心的⊙P与Rt△ABC的两条边相切.设⊙P的面积为S,你认为能否确定S的最大值?若能,请你求出S的最大值;若不能,请你说明不能确定S的最大值的理由.
考点:作图—复杂作图,切线的性质
专题:
分析:(1)利用角平分线的性质以及其作法得出即可;
(2)分别利用若⊙P与△ABC的BA、BC两条边相切,以及⊙P与△ABC的CA、AC两条边相切,若⊙P与△ABC的CA、BC两条边相切,求出半径进而比较得出答案.
(2)分别利用若⊙P与△ABC的BA、BC两条边相切,以及⊙P与△ABC的CA、AC两条边相切,若⊙P与△ABC的CA、BC两条边相切,求出半径进而比较得出答案.
解答: 解:(1)由∠B得角平分线、平角∠BXA的平分线、平角∠BYC的角平分线中的任意两条得交点即为所求圆的圆心O;
解:(1)由∠B得角平分线、平角∠BXA的平分线、平角∠BYC的角平分线中的任意两条得交点即为所求圆的圆心O;
(2)若⊙P与△ABC的BA、BC两条边相切,且面积最大,则点P为∠ABC的角平分线与AC边的交点,
作PH⊥AB于H,
∵Rt△ABC两直角边的边长为AC=3,BC=4,
∴AB=5,
则BH=BC=4,∴AH=1,
∵∠A=∠A,∠PHA=∠BCA,
∴△APH∽△ABC,
∴
=
=
,
∴PH=
AH,
在Rt△APH中,PH=
AH=
,即R1=
,
同理,⊙P与△ABC的CA、AC两条边相切,R2=
,
若⊙P与△ABC的CA、BC两条边相切,R3=
,
故R3>R2>R1,符合要求⊙P的最大面积为:
.
 解:(1)由∠B得角平分线、平角∠BXA的平分线、平角∠BYC的角平分线中的任意两条得交点即为所求圆的圆心O;
解:(1)由∠B得角平分线、平角∠BXA的平分线、平角∠BYC的角平分线中的任意两条得交点即为所求圆的圆心O;(2)若⊙P与△ABC的BA、BC两条边相切,且面积最大,则点P为∠ABC的角平分线与AC边的交点,
作PH⊥AB于H,
∵Rt△ABC两直角边的边长为AC=3,BC=4,
∴AB=5,
则BH=BC=4,∴AH=1,
∵∠A=∠A,∠PHA=∠BCA,

∴△APH∽△ABC,
∴
| AH |
| PH |
| AC |
| BC |
| 3 |
| 4 |
∴PH=
| 4 |
| 3 |
在Rt△APH中,PH=
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
同理,⊙P与△ABC的CA、AC两条边相切,R2=
| 3 |
| 2 |
若⊙P与△ABC的CA、BC两条边相切,R3=
| 12 |
| 7 |
故R3>R2>R1,符合要求⊙P的最大面积为:
| 144π |
| 49 |
点评:此题主要考查了角平分线的作法以及其性质和勾股定理等知识,得出PH=
AH是解题关键.
| 4 |
| 3 |

练习册系列答案
 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
已知a,b分别是矩形ABCD的两边,且满足a=
+
+4,若矩形的两条对角线相交所构成的锐角为α.则tanα的值为( )
| 3-b |
| b-3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 已知平面直角坐标系xOy(如图),直线y=
已知平面直角坐标系xOy(如图),直线y= 如图,在平面直角坐标系中,以点M(
如图,在平面直角坐标系中,以点M(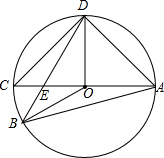 如图,AC为⊙O的直径,AC=4,B、D分别在AC两侧的圆上,∠BAD=60°,BD与AC的交点为E.
如图,AC为⊙O的直径,AC=4,B、D分别在AC两侧的圆上,∠BAD=60°,BD与AC的交点为E.