题目内容
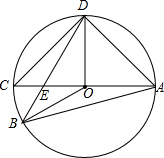 如图,AC为⊙O的直径,AC=4,B、D分别在AC两侧的圆上,∠BAD=60°,BD与AC的交点为E.
如图,AC为⊙O的直径,AC=4,B、D分别在AC两侧的圆上,∠BAD=60°,BD与AC的交点为E.(1)求∠BOD的度数及点O到BD的距离;
(2)若DE=2BE,求cos∠OED的值.
考点:垂径定理,圆周角定理,解直角三角形
专题:
分析:(1)作OH⊥BD于D,根据圆周角定理得∠BOD=2∠BAD=120°,而OB=OD,则∠ODB=30°,在Rt△ODH中,根据含30度的直角三角形三边的关系得OH=
OD=2,即点O到BD的距离为2;
(2)在Rt△ODH中据含30度的直角三角形三边的关系DH=
OH=2
,由于OH⊥BD,根据垂径定理得BH=DH=2
,即BD=4
,
而DE=2BE,则DE=
BD=
,所以HE=DE-DH=
,在Rt△OHE中,根据勾股定理计算出OE=
,然后利用余弦的定义求解.
| 1 |
| 2 |
(2)在Rt△ODH中据含30度的直角三角形三边的关系DH=
| 3 |
| 3 |
| 3 |
| 3 |
而DE=2BE,则DE=
| 2 |
| 3 |
8
| ||
| 3 |
2
| ||
| 3 |
4
| ||
| 3 |
解答:解: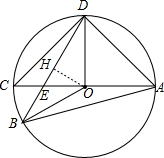 (1)作OH⊥BD于D,如图,
(1)作OH⊥BD于D,如图,
∵∠BAD=60°,
∴∠BOD=2∠BAD=2×60°=120°,
∵OB=OD,
∴∠ODB=30°,
在Rt△ODH中,OD=2,
∴OH=
OD=1,
即点O到BD的距离为1;
(2)在Rt△ODH中,∠ODB=30°,OD=2,OH=1,
∴DH=
OH=
,
∵OH⊥BD,
∴BH=DH=
,即BD=2
,
而DE=2BE,
∴DE=
BD=
,
∴HE=DE-DH=
,
在Rt△OHE中,OE=
=
,
cos∠OEH=
=
=
,
即cos∠OED的值为
.
 (1)作OH⊥BD于D,如图,
(1)作OH⊥BD于D,如图,∵∠BAD=60°,
∴∠BOD=2∠BAD=2×60°=120°,
∵OB=OD,
∴∠ODB=30°,
在Rt△ODH中,OD=2,
∴OH=
| 1 |
| 2 |
即点O到BD的距离为1;
(2)在Rt△ODH中,∠ODB=30°,OD=2,OH=1,
∴DH=
| 3 |
| 3 |
∵OH⊥BD,
∴BH=DH=
| 3 |
| 3 |
而DE=2BE,
∴DE=
| 2 |
| 3 |
4
| ||
| 3 |
∴HE=DE-DH=
2
| ||
| 3 |
在Rt△OHE中,OE=
| OH2-HE2 |
4
| ||
| 3 |
cos∠OEH=
| HE |
| OE |
| ||||
|
| 1 |
| 2 |
即cos∠OED的值为
| 1 |
| 2 |
点评:本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了圆周角定理和勾股定理.

练习册系列答案
相关题目
 如图,已知△ABC为等边三角形,AB=3,以C为圆心,1为半径作圆,P为⊙C上一动点,连AP,并绕点A顺时针旋转60°到P′,连接CP′,则CP′的取值范围是
如图,已知△ABC为等边三角形,AB=3,以C为圆心,1为半径作圆,P为⊙C上一动点,连AP,并绕点A顺时针旋转60°到P′,连接CP′,则CP′的取值范围是

 已知,如图,AO⊥BC,DO⊥OE.
已知,如图,AO⊥BC,DO⊥OE. 已知:如图,在Rt△ACB中,∠C=90°,AC=4cm,BC=3cm.点P由B出发沿BA方向向点A匀速运动;点Q由A出发沿AC方向向点C匀速运动;连接PQ.若设BP=x cm,AQ=2x cm(0<x<2),解答下列问题:
已知:如图,在Rt△ACB中,∠C=90°,AC=4cm,BC=3cm.点P由B出发沿BA方向向点A匀速运动;点Q由A出发沿AC方向向点C匀速运动;连接PQ.若设BP=x cm,AQ=2x cm(0<x<2),解答下列问题: