题目内容
问题背景:
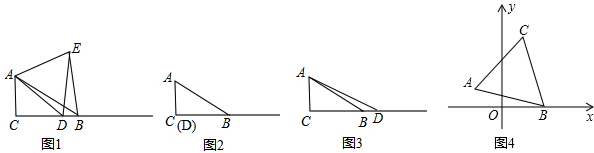
如图1,在Rt△ABC中,∠C=90°,∠ABC=30°,点D是射线CB上任意一点,△ADE是等边三角形,且点E在∠ACB的内部,连接BE.试探究线段BE与DE之间的数量关系.
探究结论:
先将图形特殊化,得出猜想,再对一般情况进行分析并加以证明.
(1)当点D与点C重合时(如图2),请你补全图形.由∠BAC的度数为 ,点E落在AB上,容易得出BE与DE之间的数量关系为 ;
(2)当点D在如图3的位置时,请你画出图形,研究线段BE与DE之间的数量关系是否与(1)中的结论相同,写出你的猜想并加以证明.
拓展应用:
(3)如图4,在平面直角坐标系x0y中,点A的坐标为(-
,1),点B是x轴上的一动点,以AB为边作等边三角形ABC.当C(x,y)在第一象限内时,求y与x的函数关系式.
如图1,在Rt△ABC中,∠C=90°,∠ABC=30°,点D是射线CB上任意一点,△ADE是等边三角形,且点E在∠ACB的内部,连接BE.试探究线段BE与DE之间的数量关系.
探究结论:
先将图形特殊化,得出猜想,再对一般情况进行分析并加以证明.
(1)当点D与点C重合时(如图2),请你补全图形.由∠BAC的度数为
(2)当点D在如图3的位置时,请你画出图形,研究线段BE与DE之间的数量关系是否与(1)中的结论相同,写出你的猜想并加以证明.
拓展应用:
(3)如图4,在平面直角坐标系x0y中,点A的坐标为(-
| 3 |

考点:一次函数综合题
专题:
分析:(1)根据题意画出图形,由直角三角形及等边三角形的性质即可得出结论;
(2)根据题意画出图形,猜想:BE=DE,取AB的中点F,连接EF,由∠ACB=90°,∠ABC=30°,可知∠1=60°,CF=AF=
AB,故△ACF是等边三角形,再由△ADE是等边三角形可得出∠CAD=∠FAE,由全等三角形的判定定理可知△ACD≌△AFE,故∠ACD=∠AFE=90°.由F是AB的中点,可知EF是AB的垂直平分线,
进而可得出△ADE是等边三角形,故DE=AE,BE=DE;
(3)根据AAS,可得△ACE与△ADB的关系,可得AE=AD,根据SAS,△ACE和△OCE的关系,可得CO=AC=CB,根据勾股定理,可得答案.
(2)根据题意画出图形,猜想:BE=DE,取AB的中点F,连接EF,由∠ACB=90°,∠ABC=30°,可知∠1=60°,CF=AF=
| 1 |
| 2 |
进而可得出△ADE是等边三角形,故DE=AE,BE=DE;
(3)根据AAS,可得△ACE与△ADB的关系,可得AE=AD,根据SAS,△ACE和△OCE的关系,可得CO=AC=CB,根据勾股定理,可得答案.
解答:解:(1)如图图中的图2,

∵∠C=90°,∠ABC=30°,
∴∠BAC=60°,
∵△ADE是等边三角形,
∴AE=CE,
∴点E落在AB的中点处;
∴AE=CE=BE=DE,
故答案为:60°,BE=DE;
(2)如图中的图3

猜想:BE=DE.
证明:取AB的中点F,连接EF,
∵∠ACB=90°,∠ABC=30°,
∴∠BAC=60°,CF=AF=
AB,
∴△ACF是等边三角形.
∴AC=AF ①
∵△ADE是等边三角形,
∴∠DAE=60°,AD=AE ②
∴∠BAC=∠DAE.
∴∠BAC+∠BAD=∠DAE+∠BAD.
即∠CAD=∠FAE③
由①②③得△ACD≌△AFE(SAS).
∴∠ACD=∠AFE=90°.
∵F是AB的中点,
∴EF是AB的垂直平分线,
∴BE=AE,
∵△ADE是等边三角形,
∴DE=AE,
∴BE=DE;
(3)如图中的图4,过A作AD⊥x轴,交x轴于D,由A(-
,1)
∴∠AOD=30°,过C分别作CE⊥OA,垂足为E,CF⊥x轴,垂足为F,
在△ACE和△ADB中,
∴△ACE≌△ADB(AAS),
∴AE=AD=1,
又∵OA=2AD=2,
∴OE=AE=1,
在△ACE和△OCE中,
∴△ACE≌△OCE(SAS),
∴CO=AC=CB,
CF⊥OB
OF=FB=x,
DB=2x+
在Rt△COF中,y2+x2=OC2
在Rt△ABD中,AB2=12+(
+2x)2,
∵AB2=OC2
∴y2=3x2+4
x+4,
∴y=±(
x+2),
∵C(x,y)在第一象限内,
∴y=-
x-2(不符合题意的要舍去)
y=
x+2.

∵∠C=90°,∠ABC=30°,
∴∠BAC=60°,
∵△ADE是等边三角形,
∴AE=CE,
∴点E落在AB的中点处;
∴AE=CE=BE=DE,
故答案为:60°,BE=DE;
(2)如图中的图3

猜想:BE=DE.
证明:取AB的中点F,连接EF,
∵∠ACB=90°,∠ABC=30°,
∴∠BAC=60°,CF=AF=
| •1 |
| 2 |
∴△ACF是等边三角形.
∴AC=AF ①
∵△ADE是等边三角形,
∴∠DAE=60°,AD=AE ②
∴∠BAC=∠DAE.
∴∠BAC+∠BAD=∠DAE+∠BAD.
即∠CAD=∠FAE③
由①②③得△ACD≌△AFE(SAS).
∴∠ACD=∠AFE=90°.
∵F是AB的中点,
∴EF是AB的垂直平分线,
∴BE=AE,
∵△ADE是等边三角形,
∴DE=AE,
∴BE=DE;
(3)如图中的图4,过A作AD⊥x轴,交x轴于D,由A(-
| 3 |

∴∠AOD=30°,过C分别作CE⊥OA,垂足为E,CF⊥x轴,垂足为F,
在△ACE和△ADB中,
|
∴△ACE≌△ADB(AAS),
∴AE=AD=1,
又∵OA=2AD=2,
∴OE=AE=1,
在△ACE和△OCE中,
|
∴△ACE≌△OCE(SAS),
∴CO=AC=CB,
CF⊥OB
OF=FB=x,
DB=2x+
| 3 |
在Rt△COF中,y2+x2=OC2
在Rt△ABD中,AB2=12+(
| 3 |
∵AB2=OC2
∴y2=3x2+4
| 3 |
∴y=±(
| 3 |
∵C(x,y)在第一象限内,
∴y=-
| 3 |
y=
| 3 |
点评:本题考查一次函数综合题,根据题意画出图形,利用数形结合求解是解答此题的关键,题目稍难.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
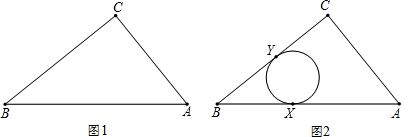
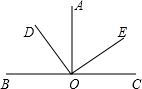 已知,如图,AO⊥BC,DO⊥OE.
已知,如图,AO⊥BC,DO⊥OE. 已知:如图,在Rt△ACB中,∠C=90°,AC=4cm,BC=3cm.点P由B出发沿BA方向向点A匀速运动;点Q由A出发沿AC方向向点C匀速运动;连接PQ.若设BP=x cm,AQ=2x cm(0<x<2),解答下列问题:
已知:如图,在Rt△ACB中,∠C=90°,AC=4cm,BC=3cm.点P由B出发沿BA方向向点A匀速运动;点Q由A出发沿AC方向向点C匀速运动;连接PQ.若设BP=x cm,AQ=2x cm(0<x<2),解答下列问题: