��Ŀ����
 ��ͼ����ƽ��ֱ������ϵ�У��Ե�M��
��ͼ����ƽ��ֱ������ϵ�У��Ե�M��| 3 |
| 2 |
| 3 |
| 2 |
��1���������ߵĽ���ʽ����N�����ꣻ
��2����ֱ��BN�Ľ���ʽ���ж�BN���M��λ�ù�ϵ����֤����
��3����P��x����һ���㣬��Q����������һ���㣮�Ƿ���������ĵ�P��Q��ʹ��A��B��P��QΪ������ı���Ϊƽ���ı��Σ������ڣ���ֱ��д����P�����꣨��д�����̣����������ڣ���˵�����ɣ�
���㣺���κ����ۺ���
ר�⣺
��������1�����ô���ϵ��������κ�������ʽ�����������䷽������������꼴�ɣ�
��2���������ֱ��BN�Ľ���ʽ������������֪�ó���ABE=��OBA+��OBE=90�㣬�����ߵ��ж��ó����ɣ�
��3�����õ�BQ1��x�ᣬ��Q1��������Ϊ��3�������ó�������꣬���������������ĵ㣬�Լ���AB��P3Q2���ı���BP3Q2A��ƽ���ı��Σ�����������ɣ�
��2���������ֱ��BN�Ľ���ʽ������������֪�ó���ABE=��OBA+��OBE=90�㣬�����ߵ��ж��ó����ɣ�
��3�����õ�BQ1��x�ᣬ��Q1��������Ϊ��3�������ó�������꣬���������������ĵ㣬�Լ���AB��P3Q2���ı���BP3Q2A��ƽ���ı��Σ�����������ɣ�
����⣺��1����ͼ1����MC��OA��C����MD��OB��D����C��
��0����D��0��
��
��MΪԲ�ģ�
��OA=2OC=3��OB=2OD=3��
��A��3��0����B��0��3����
��
��
���
��
�������߽���ʽΪy=-x2+2x+3��
��y=-x2+2x+3=-��x-1��2+4��
��N��1��4����
��2����ֱ��BN�Ľ���ʽΪy=kx+m��
���������
��
���
��
��ֱ��BN�Ľ���ʽΪy=x+3��
ֱ��BN���M���У�
֤������ֱ��BN��x���ཻ�ڵ�E��
��y=x+3=0����x=-3������E��-3��0����
��OE=OB=OA��
�ߡ�AOB=��BOE=90�㣬
��ABΪ��Mֱ����
��OBA=��OBE=45�㣬
���ABE=��OBA+��OBE=90�㣬
��ֱ��BN���M���У�
��3�����ڣ�
��BQ1��x�ᣬ��Q1��������Ϊ��3��
��3=-��x-1��2+4��
��ã�x1=0��x2=2��
��Q1��2��3����
��BQ1=2��
���ı���BAP2Q1��ƽ���ı��Σ�
��AP2=2��
��P2��5��0����
ͬ���ɵó���P1��1��0����
��AB��P3Q2��
�ı���BP3Q2A��ƽ���ı��Σ�
����ֱ��AB�Ľ���ʽΪ��y=dx+e��
��
��
��ã�
��
��ֱ��AB�Ľ���ʽΪ��y=-x+3��
��ֱ��P3Q2�Ľ���ʽΪ��y=-x+f��
������ɵó���Q2������Ϊ��-3��
�����������-3=-x2+2x+3��
��ã�x=1��
��
��Q2��1+
��-3����
��-3=-��1+
��+f��
��ã�f=-2+
��
��y=-x-2+
��
��P3��-2+
��0����
ͬ���ɵó���P4��-2-
��0����
������������������P��������P1��1��0����P2��5��0����P3��-2+
��0����P4��-2-
��0����
| 3 |
| 2 |
| 3 |
| 2 |
��MΪԲ�ģ�
��OA=2OC=3��OB=2OD=3��
��A��3��0����B��0��3����
��
|
���
|
�������߽���ʽΪy=-x2+2x+3��
��y=-x2+2x+3=-��x-1��2+4��
��N��1��4����

��2����ֱ��BN�Ľ���ʽΪy=kx+m��
���������
|
���
|
��ֱ��BN�Ľ���ʽΪy=x+3��
ֱ��BN���M���У�
֤������ֱ��BN��x���ཻ�ڵ�E��
��y=x+3=0����x=-3������E��-3��0����
��OE=OB=OA��
�ߡ�AOB=��BOE=90�㣬
��ABΪ��Mֱ����
��OBA=��OBE=45�㣬
���ABE=��OBA+��OBE=90�㣬
��ֱ��BN���M���У�
��3�����ڣ�
��BQ1��x�ᣬ��Q1��������Ϊ��3��
��3=-��x-1��2+4��
��ã�x1=0��x2=2��
��Q1��2��3����
��BQ1=2��
���ı���BAP2Q1��ƽ���ı��Σ�
��AP2=2��
��P2��5��0����
ͬ���ɵó���P1��1��0����
��AB��P3Q2��
�ı���BP3Q2A��ƽ���ı��Σ�

����ֱ��AB�Ľ���ʽΪ��y=dx+e��
��
|
��ã�
|
��ֱ��AB�Ľ���ʽΪ��y=-x+3��
��ֱ��P3Q2�Ľ���ʽΪ��y=-x+f��
������ɵó���Q2������Ϊ��-3��
�����������-3=-x2+2x+3��
��ã�x=1��
| 7 |
��Q2��1+
| 7 |
��-3=-��1+
| 7 |
��ã�f=-2+
| 7 |
��y=-x-2+
| 7 |
��P3��-2+
| 7 |
ͬ���ɵó���P4��-2-
| 7 |
������������������P��������P1��1��0����P2��5��0����P3��-2+
| 7 |
| 7 |
������������Ҫ�����˶��κ����ۺ�Ӧ���Լ�ƽ���ı��ε��������ж���֪ʶ�����÷��������Լ����ν�ϵó��ǽ���ؼ���

��ϰ��ϵ�д�
 ���Ͱ�ͨ������ϵ�д�
���Ͱ�ͨ������ϵ�д� �ٷ�ѧ����ҵ��������ϵ�д�
�ٷ�ѧ����ҵ��������ϵ�д�
�����Ŀ
��
������������xһ���ǣ�������
| x2 |
| A����ʵ�� | B�������� |
| C���������� | D����ȫƽ���� |
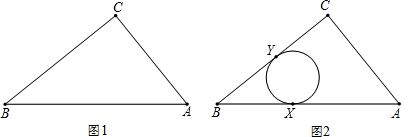
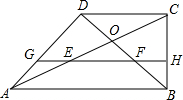 ��ֱ������ABCD�У�AB��CD����ABC=90�㣬AB=2BC=2CD���Խ���AC��BD�ཻ�ڵ�O���߶�OA��OB���е�ֱ�ΪE��F��
��ֱ������ABCD�У�AB��CD����ABC=90�㣬AB=2BC=2CD���Խ���AC��BD�ཻ�ڵ�O���߶�OA��OB���е�ֱ�ΪE��F��  ��ͼ����M��Rt��ABC��б��BC�ϲ���B��C�غϵ�һ���㣬����M��ֱ�߽ء�ABC��ʹ�صõ���������ԭ��ABC���ƣ�������ֱ�߹���
��ͼ����M��Rt��ABC��б��BC�ϲ���B��C�غϵ�һ���㣬����M��ֱ�߽ء�ABC��ʹ�صõ���������ԭ��ABC���ƣ�������ֱ�߹���