题目内容
已知a,b分别是矩形ABCD的两边,且满足a=
+
+4,若矩形的两条对角线相交所构成的锐角为α.则tanα的值为( )
| 3-b |
| b-3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:矩形的性质,二次根式有意义的条件,锐角三角函数的定义
专题:
分析:首先过点A作AE⊥OB于点E,过点O作OF⊥AB于点F,由a=
+
+4,可求得a与b的值,继而由勾股定理求得AC的长,然后由三角形的面积,求得OF的长,继而求得答案.
| 3-b |
| b-3 |
解答: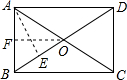 解:过点A作AE⊥OB于点E,过点O作OF⊥AB于点F,
解:过点A作AE⊥OB于点E,过点O作OF⊥AB于点F,
根据题意得:
,
解得:b=3,
∴a=4,
∵四边形ABCD是矩形,
∴AC=
=5,
∴OA=OB=
,
∴AF=BF=
AB=
,
∴OF=
=2,
∵S△AOB=
AB•OF=
OB•AE,
∴AE=
=
=
,
∴OE=
=0.7,
∴tanα=
=
.
故选A.
 解:过点A作AE⊥OB于点E,过点O作OF⊥AB于点F,
解:过点A作AE⊥OB于点E,过点O作OF⊥AB于点F,根据题意得:
|
解得:b=3,
∴a=4,
∵四边形ABCD是矩形,
∴AC=
| a2+b2 |
∴OA=OB=
| 5 |
| 2 |
∴AF=BF=
| 1 |
| 2 |
| 3 |
| 2 |
∴OF=
| OA2-AF2 |
∵S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
∴AE=
| AB•OF |
| OB |
| 2×3 | ||
|
| 12 |
| 5 |
∴OE=
| OA2-AE2 |
∴tanα=
| AE |
| OE |
| 24 |
| 7 |
故选A.
点评:此题考查了矩形的性质、三角形的面积问题以及勾股定理等知识.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
若
是有理数,则x一定是( )
| x2 |
| A、正实数 | B、有理数 |
| C、正有理数 | D、完全平方数 |
 如图,已知△ABC为等边三角形,AB=3,以C为圆心,1为半径作圆,P为⊙C上一动点,连AP,并绕点A顺时针旋转60°到P′,连接CP′,则CP′的取值范围是
如图,已知△ABC为等边三角形,AB=3,以C为圆心,1为半径作圆,P为⊙C上一动点,连AP,并绕点A顺时针旋转60°到P′,连接CP′,则CP′的取值范围是
 已知:如图,在Rt△ACB中,∠C=90°,AC=4cm,BC=3cm.点P由B出发沿BA方向向点A匀速运动;点Q由A出发沿AC方向向点C匀速运动;连接PQ.若设BP=x cm,AQ=2x cm(0<x<2),解答下列问题:
已知:如图,在Rt△ACB中,∠C=90°,AC=4cm,BC=3cm.点P由B出发沿BA方向向点A匀速运动;点Q由A出发沿AC方向向点C匀速运动;连接PQ.若设BP=x cm,AQ=2x cm(0<x<2),解答下列问题: