题目内容
7.如图,在正方形ABCD中,点E在射线AB上,点F在射线AD上.(1)若CE⊥CF,求证:CE=CF;
(2)若CE=CF,则CE⊥CF是否成立?若成立,请给出证明,若不成立,请画图说明.
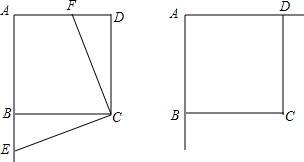
分析 (1)首先由正方形的性质得CB=CD,利用全等三角形的ASA判定得△BCE和△DCF全等,由全等三角形的性质得出结论;
(2)根据正方形的性质和全等三角形的判定和性质进行证明即可.
解答 (1)证明:∵四边形ABCD是正方形
∴CB=CD,∠ABC=∠BCD=∠D=90°
∵CE⊥CF
∴∠ECF=90°
∴∠BCE=∠DCF=90°-∠BCF
在△BCE和△DCF中,
$\left\{\begin{array}{l}{∠CBE=∠D=90°}\\{BC=DC}\\{∠BCE=∠DCF}\end{array}\right.$,
∴△BCE≌△DCF,
∴CE=CF.
(2)若CE=CF,则CE⊥CF不一定成立
当点E在线段AB上,且点F在AD延长线上或当点E在AB延长线上,且点F在线段AD上时CE⊥CF成立,证明如下:
∵四边形ABCD是正方形
∴CB=CD,∠ABC=∠BCD=∠D=90°
∵CE⊥CF
∴∠ECF=90°
∴∠BCE=∠DCF=90°-∠BCF
在△BCE和△DCF中,
$\left\{\begin{array}{l}{∠CBE=∠D=90°}\\{BC=DC}\\{∠BCE=∠DCF}\end{array}\right.$,
∴△BCE≌△DCF,
∴CE=CF;
当点E在线段AB上,且点F在线段AD上或当点E在线段AB延长线上,且点F在AD延长线上时,CE⊥CF不成立,如图如下: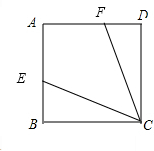 .
.
点评 本题主要考查了正方形的性质,全等三角形的判定,结合图形,综合利用各定理是解答此题的关键.

练习册系列答案
相关题目
15.已知(a+b)2=7,(a-b)2=4,则a2+b2的值为( )
| A. | 11 | B. | 3 | C. | $\frac{3}{2}$ | D. | $\frac{11}{2}$ |
12.下列事件是必然事件的是( )
| A. | 打开电视正在播广告 | B. | 没有水分,种子发芽 | ||
| C. | 367人中至少有2人的生日相同 | D. | 3天内将下雨 |
19.如图,在Rt△ABC中,∠ACB=90°,D为斜边AB的中点,动点P从B点出发,沿B→C→A运动.如图(1)所示,设S△DPB=y,点P运动的路程为x,若y与x之间的函数图象如图(2)所示,则图(2)中Q点的坐标是( )
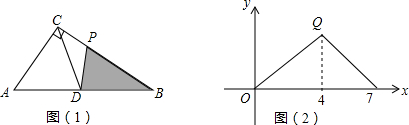

| A. | (4,4) | B. | (4,3) | C. | (4,6) | D. | (4,12) |
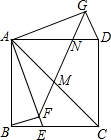 如图,正方形ABCD中,AB=3$\sqrt{10}$,E为BC上一点,且CE=2BE,BF垂直AE于F,将△ABF绕点A旋转,使AB与AD重合,得到△AGD,连接GF交AC于M,交AD于N,则MN的长为$\frac{15}{4}$$\sqrt{2}$.
如图,正方形ABCD中,AB=3$\sqrt{10}$,E为BC上一点,且CE=2BE,BF垂直AE于F,将△ABF绕点A旋转,使AB与AD重合,得到△AGD,连接GF交AC于M,交AD于N,则MN的长为$\frac{15}{4}$$\sqrt{2}$.