题目内容
2.计算(1)(x+2y)(x-2y)+(x+1)(x-1)
(2)(2x-y)2-4(x-y)(x+2y)
(3)(2x2y)3•(-7xy2)÷14x4y3
(4)1232-124×122.
分析 (1)根据平方差公式计算,再合并同类项即可求解;
(2)根据多项式乘以多项式的计算法则和完全平方公式计算,再合并同类项即可求解;
(3)根据单项式的乘除法法则计算即可求解;
(4)根据平方差公式计算即可求解.
解答 解:(1)(x+2y)(x-2y)+(x+1)(x-1)
=x2-4y2+x2-1
=2x2-4y2-1;
(2)(2x-y)2-4(x-y)(x+2y)
=4x2-4xy+y2-4(x2+2xy-xy-2y2)
=9y2-8xy;
(3)(2x2y)3•(-7xy2)÷14x4y3=-4x3y2;
(4)1232-124×122
=1232-(123+1)(123-1)
=1232-(1232-1)
=1.
点评 此题考查了整式的混合运算,涉及的知识有:平方,零指数幂和负整数指数幂,多项式乘以多项式,单项式乘以单项式,完全平方公式,平方差公式,去括号法则,以及合并同类项法则,熟练掌握公式及法则是解本题的关键.

练习册系列答案
相关题目
10.下列各式中,不能用平方差公式因式分解的是( )
| A. | -a2-4b2 | B. | -1+25a2 | C. | $\frac{1}{16}$-9a2 | D. | -a4+1 |
17. 如图,正△ABC的边长是2,分别以点B、C为圆心,以r为半径作两条弧,设两弧与边BC围成的阴影部分面积为S,当$\sqrt{2}≤r<2$时,S的取值范围是( )
如图,正△ABC的边长是2,分别以点B、C为圆心,以r为半径作两条弧,设两弧与边BC围成的阴影部分面积为S,当$\sqrt{2}≤r<2$时,S的取值范围是( )
 如图,正△ABC的边长是2,分别以点B、C为圆心,以r为半径作两条弧,设两弧与边BC围成的阴影部分面积为S,当$\sqrt{2}≤r<2$时,S的取值范围是( )
如图,正△ABC的边长是2,分别以点B、C为圆心,以r为半径作两条弧,设两弧与边BC围成的阴影部分面积为S,当$\sqrt{2}≤r<2$时,S的取值范围是( )| A. | $\frac{π}{2}$-1≤S<$\frac{4π}{3}$-$\sqrt{3}$ | B. | $\frac{π}{2}$-1≤S<$\frac{4π}{3}$-1 | C. | 1≤S<$\sqrt{3}$ | D. | $\sqrt{3}≤S$$<2\sqrt{3}$-1 |
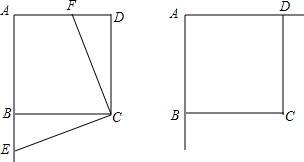
 如图,AB∥CD且∠A=25°,∠C=45°,则∠E=70°.
如图,AB∥CD且∠A=25°,∠C=45°,则∠E=70°.