题目内容
19.如图,在Rt△ABC中,∠ACB=90°,D为斜边AB的中点,动点P从B点出发,沿B→C→A运动.如图(1)所示,设S△DPB=y,点P运动的路程为x,若y与x之间的函数图象如图(2)所示,则图(2)中Q点的坐标是( )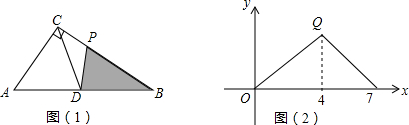
| A. | (4,4) | B. | (4,3) | C. | (4,6) | D. | (4,12) |
分析 根据已知条件和图象可以得到BC、AC的长度,当x=4时,点P与点C重合,此时△DPC的面积等于△ABC面积的一半,从而可以求出点Q的坐标,本题得以解决.
解答 解:根据题意和图象可得,
BC=4,AC=7-4=3,
∵∠ACB=90°,点D为AB的中点,
∴当x=4时,${S}_{△DPB}=\frac{{S}_{△ACB}}{2}$,
∴y=$\frac{3×4}{2}×\frac{1}{2}=3$,
即点Q的坐标是(4,3),
故选B.
点评 本题考查动点问题的函数图象,解题的关键是明确题意,利用数形结合的思想解答问题.

练习册系列答案
相关题目
9.下列根式中,最简二次根式是( )
| A. | $\sqrt{{m}^{2}+{n}^{2}}$ | B. | $\sqrt{16m}$ | C. | $\sqrt{\frac{m}{2}}$ | D. | $\sqrt{0.5}$ |
10.下列各式中,不能用平方差公式因式分解的是( )
| A. | -a2-4b2 | B. | -1+25a2 | C. | $\frac{1}{16}$-9a2 | D. | -a4+1 |
4.下列各组线段能构成直角三角形的一组是( )
| A. | 7,12,13 | B. | 30,40,50 | C. | 5,9,12 | D. | 3,4,6 |
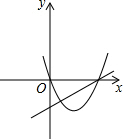
 如图,方格纸中的每个小方格是边长为1个单位长度的正方形.
如图,方格纸中的每个小方格是边长为1个单位长度的正方形.