题目内容
18.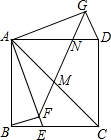 如图,正方形ABCD中,AB=3$\sqrt{10}$,E为BC上一点,且CE=2BE,BF垂直AE于F,将△ABF绕点A旋转,使AB与AD重合,得到△AGD,连接GF交AC于M,交AD于N,则MN的长为$\frac{15}{4}$$\sqrt{2}$.
如图,正方形ABCD中,AB=3$\sqrt{10}$,E为BC上一点,且CE=2BE,BF垂直AE于F,将△ABF绕点A旋转,使AB与AD重合,得到△AGD,连接GF交AC于M,交AD于N,则MN的长为$\frac{15}{4}$$\sqrt{2}$.
分析 由旋转得到结论判断出△AFG是等腰直角三角形,再有你三角形相似计算即可
解答 解:根据旋转得,∠GAF=DAB=90°,AG=AF,DG=BF,
∴△AFG是等腰直角三角形,
在Rt△ABE中,AB=$\sqrt{10}$,BE=$\sqrt{10}$,
∴AE=10,
∵△ABE∽BFE,
∴$\frac{AE}{BE}=\frac{AB}{BF}$,
∴BF=$\frac{AB×BE}{AE}$=3=DG,
∴AG=AF=9,
∴GF=9$\sqrt{2}$,
∵△ACE∽AFM,
∴$\frac{AC}{AF}=\frac{CE}{FM}$,
∴FM=3$\sqrt{2}$,
∵△AFN∽△DGN,
∴$\frac{FN}{GN}=\frac{AF}{DG}$,
∴FN=3GN,
∴GN=$\frac{1}{4}$FG=$\frac{9\sqrt{2}}{4}$,
∴MN=FG-FM-GN=$\frac{15\sqrt{2}}{4}$,
故答案为$\frac{15\sqrt{2}}{4}$
点评 此题是旋转的性质题,主要考查了旋转的性质,三角形相似的性质,解本题的关键是三角形相似得到的比例式求线段.

练习册系列答案
相关题目
9.下列根式中,最简二次根式是( )
| A. | $\sqrt{{m}^{2}+{n}^{2}}$ | B. | $\sqrt{16m}$ | C. | $\sqrt{\frac{m}{2}}$ | D. | $\sqrt{0.5}$ |
6.现给出四个命题:①等边三角形既是轴对称图形,又是中心对称图形;②相似三角形的面积比等于它们的相似比;③菱形的面积等于两条对角线的积;④一组数据2,5,4,3,3的中位数是4,众数是3,其中不正确的命题的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10.下列各式中,不能用平方差公式因式分解的是( )
| A. | -a2-4b2 | B. | -1+25a2 | C. | $\frac{1}{16}$-9a2 | D. | -a4+1 |




 如图,方格纸中的每个小方格是边长为1个单位长度的正方形.
如图,方格纸中的每个小方格是边长为1个单位长度的正方形.