题目内容
17.(1)解方程:x2-4x+1=0;(2)解方程组:$\left\{\begin{array}{l}x-3y=1,…①\\ 2(x-3)=y+6.…②\end{array}$.
分析 (1)方程利用公式法求出解即可;
(2)方程组利用加减消元法求出解即可.
解答 解:(1)这里a=1,b=-4,c=1,
∵△=16-4=12,
∴x=$\frac{4±\sqrt{16-4}}{2}$,
∴x=2±$\sqrt{3}$;
(2)由①,得x=1+3y③,
由②,得2x-y=12④,
把③代入④得2+6y-y=12,
解得:y=2,
把y=2代入③得x=7,
∴方程组的解为$\left\{\begin{array}{l}x=7\\ y=2\end{array}$.
点评 此题考查了解二元一次方程组,以及解一元二次方程-公式法,熟练掌握运算法则是解本题的关键.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
18.下列计算中,正确的是( )
| A. | 2x2•3x3=6x6 | B. | 2x2+3x3=5x5 | C. | 2x2•3x3=6x5 | D. | 2x3-3x2=-x |
 如图,方格纸中的每个小方格是边长为1个单位长度的正方形.
如图,方格纸中的每个小方格是边长为1个单位长度的正方形.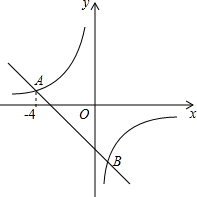 在平面直角坐标系xOy中,一次函数y=-x+k的图象与反比例函数y=-$\frac{4}{x}$的图象交于点A(-4,n)和点B.
在平面直角坐标系xOy中,一次函数y=-x+k的图象与反比例函数y=-$\frac{4}{x}$的图象交于点A(-4,n)和点B.