题目内容
8.已知关于x的不等式(1-a)x>2,两边都除以(1-a),得x<$\frac{2}{1-a}$,试化简:|a-1|+|a+2|.分析 不等式的两边同时乘以(或除以)同一个负数,不等号的方向改变,由(1-a)x>2,两边都除以(1-a),得x<$\frac{2}{1-a}$,可得1-a<0,所以a>1;然后根据绝对值的求法,求出|a-1|+|a+2|的值是多少即可.
解答 解:∵由(1-a)x>2,两边都除以(1-a),得x<$\frac{2}{1-a}$,
∴1-a<0,
∴a>1,
∴|a-1|+|a+2|
=(a-1)+(a+2)
=2a+1.
点评 此题主要考查了不等式的基本性质:(1)不等式的两边同时乘以(或除以)同一个正数,不等号的方向不变;(2)不等式的两边同时乘以(或除以)同一个负数,不等号的方向改变;(3)等式的两边同时加上(或减去)同一个数或同一个含有字母的式子,不等号的方向不变.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
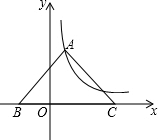 如图,等腰Rt△ABC的斜边BC在x轴上,顶点A在反比例函数y=$\frac{4}{x}$(x>0)的图象上,则OC2-OB2的值为16.
如图,等腰Rt△ABC的斜边BC在x轴上,顶点A在反比例函数y=$\frac{4}{x}$(x>0)的图象上,则OC2-OB2的值为16. 已知在一个5×5的正方形网格中(正方形的边长为1个单位长度)有一个格点△ABC(三角形的各顶点是网格线的交点),且AB=2$\sqrt{5}$,BC=$\sqrt{5}$,AC=5.
已知在一个5×5的正方形网格中(正方形的边长为1个单位长度)有一个格点△ABC(三角形的各顶点是网格线的交点),且AB=2$\sqrt{5}$,BC=$\sqrt{5}$,AC=5.