题目内容
18．
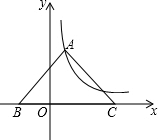如图，等腰Rt△ABC的斜边BC在x轴上，顶点A在反比例函数y=$\frac{4}{x}$（x＞0）的图象上，则OC2-OB2的值为16．
分析 作AH⊥BC于H，如图，根据反比例函数图象上点的坐标特征可设A（t，$\frac{4}{t}$），则根据等腰直角三角形的性质得到AH=BH=CH=$\frac{4}{t}$，所以OC+OB=$\frac{8}{t}$，OC=$\frac{4}{t}$+t，OB=$\frac{4}{t}$-t，则OC-OB=2t，
然后利用平方差公式得到OC2-OB2=（OC+OB）（OC-OB），再利用整体代入的方法计算即可．
解答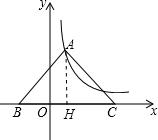 
解：作AH⊥BC于H，如图，设A（t，$\frac{4}{t}$），
∵△ABC为等腰直角三角形，
∴AH=BH=CH，即BH=AH=$\frac{4}{t}$，
∴OC+OB=BC=$\frac{8}{t}$，OC=CH+OH=$\frac{4}{t}$+t，OB=BH-OH=$\frac{4}{t}$-t，
∴OC-OB=2t，
∴OC2-OB2=（OC+OB）（OC-OB）=$\frac{8}{t}$×2t=16．
故答案为16．
点评 本题考查了反比例函数图象上点的坐标特征：反比例函数y=$\frac{k}{x}$（k为常数，k≠0）的图象是双曲线，图象上的点（x，y）的横纵坐标的积是定值k，即xy=k．也考查了等腰直角三角形的性质．
练习册系列答案
相关题目
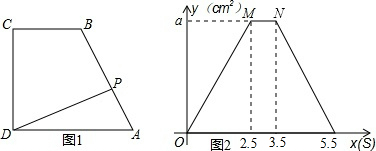
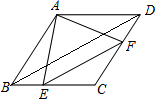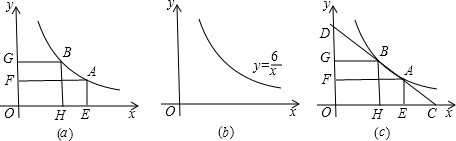
如图，在菱形ABCD中，∠ABC中，∠ABC=60°，点E、F分别从点B、D同时出发，以同样的速度沿边BC、DC向点C运动（点E、F不与点B、D重合）．给出以下四个结论：①AE=AF；②EF∥BD；③当点E、F分别为边BC、DC的中点时，EF=$\sqrt{3}$BE；④当点E、F分别为边BC、DC的中点时，△AEF的面积最大．上述结论中正确的个数有（ ）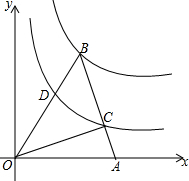
如图，坐标系中，AB⊥x轴于A点，双曲线y=$\frac{{k}_{1}}{x}$过点B，反比例函数y=$\frac{{k}_{2}}{x}$过C，D点且OD=BC，已知B（2，3），则D点坐标为（$\frac{-\sqrt{13}+7}{3}$，$\frac{-\sqrt{13}+7}{2}$）．