题目内容
16．
已知在一个5×5的正方形网格中（正方形的边长为1个单位长度）有一个格点△ABC（三角形的各顶点是网格线的交点），且AB=2$\sqrt{5}$，BC=$\sqrt{5}$，AC=5．（1）请在网格中画出一个符合条件的△ABC（不要求写画法）；
（2）△ABC是不是直角三角形？说明理由．
分析 （1）根据题意画出图形即可；
（2）根据勾股定理进行判断即可．
解答 解：（1）如图所示；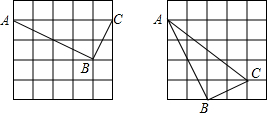
；
（2）△ABC是直角三角形．
∵AB2+BC2=（2$\sqrt{5}$）2+（$\sqrt{5}$）2=20+5=25，AC2=52=25，
∴AB2+BC2=AC2，
∴△ABC是直角三角形．
点评 本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
练习册系列答案
相关题目
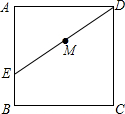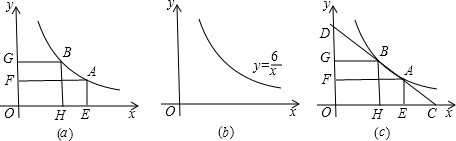
如图，点E在正方形ABCD的边AB上，AE=3，BE=1，点M是DE的中点，若点P在正方形ABCD的边上，且PM=2.5，则符合条件的点P的个数是（ ）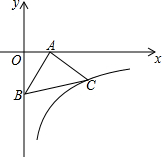
如图，在等腰三角形ABC中，∠BAC=90°，点A、B分别在x轴正半轴上和y轴的负半轴上，点A的坐标为（3，0），反比例函数y=$\frac{k}{x}$（x＞0）的图象经过点C（7，n），则k的值为（ ）
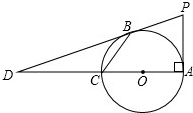如图所示，AC为⊙O的直径且PA⊥AC，BC是⊙O的一条弦，直线PB交直线AC于点D，且PB=PA．