题目内容
18.已知多项式2x4-3x3+ax2+7x+b含有因式x2+x-2,求$\frac{a}{b}$的值.分析 由于x2+x-2=(x+2)(x-1),而多项式2x4-3x3+ax2+7x+b能被x2+x-2整除,则2x4-3x3+ax2+7x+b能被(x+2)(x-1)整除.运用待定系数法,可设商是A,则2x4-3x3+ax2+7x+b=A(x+2)(x-1),则x=-2和x=1时,2x4-3x3+ax2+7x+b=0,分别代入,得到关于a、b的二元一次方程组,解此方程组,求出a、b的值,进而得到$\frac{a}{b}$的值.
解答 解:∵x2+x-2=(x+2)(x-1),
∴2x4-3x3+ax2+7x+b能被(x+2)(x-1)整除,
设商是A.
则2x4-3x3+ax2+7x+b=A(x+2)(x-1),
则x=-2和x=1时,右边都等于0,所以左边也等于0.
当x=-2时,2x4-3x3+ax2+7x+b=32+24+4a-14+b=4a+b+42=0 ①
当x=1时,2x4-3x3+ax2+7x+b=2-3+a+7+b=a+b+6=0 ②
①-②,得
3a+36=0,
∴a=-12,
∴b=-6-a=6.
∴$\frac{a}{b}$=$\frac{-12}{6}$=-2.
点评 本题主要考查了待定系数法在因式分解中的应用,注意因式的特点,灵活解决问题.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
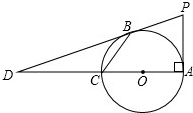 如图所示,AC为⊙O的直径且PA⊥AC,BC是⊙O的一条弦,直线PB交直线AC于点D,且PB=PA.
如图所示,AC为⊙O的直径且PA⊥AC,BC是⊙O的一条弦,直线PB交直线AC于点D,且PB=PA.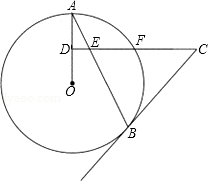 AB是⊙O的弦,D为半径OA的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.
AB是⊙O的弦,D为半径OA的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB. 如图,已知四边形ABCD是平行四边形,延长AB至F,使BF=AB,连接DF交BC于点E,S△AEF=24,求△CEF的面积.
如图,已知四边形ABCD是平行四边形,延长AB至F,使BF=AB,连接DF交BC于点E,S△AEF=24,求△CEF的面积.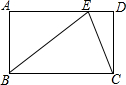 已知:如图,点E是矩形ABCD的边AD上一点,BE=AD,AE=8,现有甲乙两人同时从E点出发,分别沿EC,ED方向前进,甲的速度是乙的$\sqrt{10}$倍,甲到达目的地C点的同时乙恰好到达终点D处.
已知:如图,点E是矩形ABCD的边AD上一点,BE=AD,AE=8,现有甲乙两人同时从E点出发,分别沿EC,ED方向前进,甲的速度是乙的$\sqrt{10}$倍,甲到达目的地C点的同时乙恰好到达终点D处.