题目内容
11．（1）化简：$\frac{a+b-b}{{a}^{2}-{b}^{2}}$÷$\frac{a}{a+b}$（2）解不等式组：$\left\{\begin{array}{l}{3（x-1）≤5x+1}\\{\frac{x-1}{2}≥2x-4}\end{array}\right.$．
分析 （1）原式利用除法法则变形，约分即可得到结果；
（2）分别求出不等式组中两不等式的解集，找出两解集的公共部分即可．
解答 解：（1）原式=$\frac{a}{（a+b）（a-b）}$•$\frac{a+b}{a}$=$\frac{1}{a-b}$；
（2）$\left\{\begin{array}{l}{3（x-1）≤5x+1①}\\{\frac{x-1}{2}≥2x-4②}\end{array}\right.$，
由①得：x≥-2，
由②得：x≤$\frac{7}{3}$，
则不等式组的解集为-2≤x≤$\frac{7}{3}$．
点评 此题考查了分式的乘除法，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
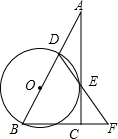在Rt△ABC中，∠ACB=90°，D是AB边上的一点，以BD为直径作⊙O交AC于点E，连结DE并延长，与BC的延长线交于点F，且BD=BF．
如图，在△ABC中，∠A=60°，BM⊥AC于点M，CN⊥AB于点N，P为BC边的中点，连接PM，PN，则下列结论中，正确的个数是（ ）
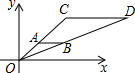如图，在直角坐标系中，△OAB和△OCD是位似图形，O为位似中心，若A点的坐标为（1，1），B点的坐标为（2，1），C点的坐标为（3，3），那么点D的坐标是（6，3）．
20．
如图，点N1，N2，…，N8将圆周八等分，连接N1N2，、N1N8、N4N5后，再连接一对相邻的两点后，形成的图形不是轴对称图形，则连接的这条线段可能是（ ）
如图，点N1，N2，…，N8将圆周八等分，连接N1N2，、N1N8、N4N5后，再连接一对相邻的两点后，形成的图形不是轴对称图形，则连接的这条线段可能是（ ）| A． | N2N3 | B． | N3N4 | C． | N5N6 | D． | N7N8 |
建模是数学的核心素养之一，小明在计算$\frac{1}{3}$+$\frac{1}{{3}^{2}}$+$\frac{2}{{3}^{3}}$+…+$\frac{1}{{3}^{n}}$时利用了如下的正方形模型．