题目内容
1. 建模是数学的核心素养之一,小明在计算$\frac{1}{3}$+$\frac{1}{{3}^{2}}$+$\frac{2}{{3}^{3}}$+…+$\frac{1}{{3}^{n}}$时利用了如下的正方形模型.
建模是数学的核心素养之一,小明在计算$\frac{1}{3}$+$\frac{1}{{3}^{2}}$+$\frac{2}{{3}^{3}}$+…+$\frac{1}{{3}^{n}}$时利用了如下的正方形模型.第1次分割,把正方形的面积三等分,阴影部分的面积为$\frac{2}{3}$;
第2次分割,把上次分割图中空白部分的面积继续三等分,阴影部分的面积之和为$\frac{2}{3}$+$\frac{2}{{3}^{2}}$;
第3次分割,把上次分割图中空白部分的面积继续三等分,…;
…
由此计算$\frac{1}{3}$+$\frac{1}{{3}^{2}}$+$\frac{1}{{3}^{3}}$+…+$\frac{1}{{3}^{n}}$的结果是$\frac{1}{2}$-$\frac{1}{2×{3}^{n}}$(用含n的代数式表示)
分析 由阴影部分面积=1-空白部分面积,可得第n次分割图中:$\frac{2}{3}+\frac{2}{{3}^{2}}+\frac{2}{{3}^{2}}+…+\frac{2}{{3}^{n}}$=1-$\frac{1}{{3}^{n}}$,两边除以2可得答案.
解答 解:第1次分割,阴影部分的面积为$\frac{2}{3}$,空白部分面积为1-$\frac{2}{3}$=$\frac{1}{3}$;
第2次分割,阴影部分的面积之和为$\frac{2}{3}$+$\frac{2}{{3}^{2}}$,空白部分面积为1-($\frac{2}{3}$+$\frac{2}{{3}^{2}}$)=$\frac{1}{{3}^{2}}$;
第3次分割,把上次分割图中空白部分的面积继续三等分,…;
…
第n次分割,所有阴影部分的面积之和为$\frac{2}{3}+\frac{2}{{3}^{2}}+\frac{2}{{3}^{2}}+…+\frac{2}{{3}^{n}}$,最后空白部分的面积是$\frac{1}{{3}^{n}}$.
根据第n次分割图可得等式:$\frac{2}{3}+\frac{2}{{3}^{2}}+\frac{2}{{3}^{2}}+…+\frac{2}{{3}^{n}}$=1-$\frac{1}{{3}^{n}}$,
两边同除以2,得$\frac{1}{3}$+$\frac{1}{{3}^{2}}$+$\frac{1}{{3}^{3}}$+…+$\frac{1}{{3}^{n}}$=$\frac{1}{2}$-$\frac{1}{2×{3}^{n}}$.
故答案为:$\frac{1}{2}$-$\frac{1}{2×{3}^{n}}$.
点评 本题考查了图形的变化规律,读懂题目信息,理解分割的方法以及求和的方法是解题的关键.

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案| A. | 5 | B. | $\frac{1}{5}$ | C. | -5 | D. | -$\frac{1}{5}$ |
| A. | 平行四边形的对角线互相平分 | |
| B. | 对角线互相垂直平分的四边形是菱形 | |
| C. | 矩形的对角线相等 | |
| D. | 对角线相等的四边形是正方形 |
| A. | 30° | B. | 45° | C. | 60° | D. | 70° |
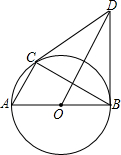 如图,⊙O是Rt△ABC的外接圆,点O在AB上,BD⊥AB,点B是垂足,OD∥AC,连接CD.
如图,⊙O是Rt△ABC的外接圆,点O在AB上,BD⊥AB,点B是垂足,OD∥AC,连接CD.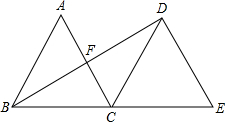 如图,将边长为2的等边三角形ABC绕点C旋转120°,得到△DCE,连接BD,则BD的长是2$\sqrt{3}$.
如图,将边长为2的等边三角形ABC绕点C旋转120°,得到△DCE,连接BD,则BD的长是2$\sqrt{3}$.