题目内容
在直角三角形中，各边的长度都扩大3倍，则锐角A的三角函数值
A. 也扩大3倍 B. 缩小为原来的
C. 都不变 D. 有的扩大，有的缩小
C
【解析】试题分析：根据锐角三角函数的概念，可知在直角三角形中，各边的长度都扩大3倍，锐角A的三角函数值不变．
故选C．
练习册系列答案
提分百分百检测卷系列答案
相关题目
下面用代数式表示正确的是（ ）
A. -a的平方表示为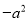
B. a与比a大2的数的积表示为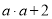
C. a与b的和的平方表示为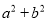
D. a，b两数差的平方表示为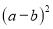
D
【解析】试题分析：A、－a的平方表示为(－a)2，故此选项错误；
B、a与比a大2的数的积表示为a(a＋2)，故此选项错误；
C、a与b的和的平方表示为(a＋b)2，故此选项错误；
D、a，b两数差的平方表示为(a－b)2，故此选项错误．
故选D． 黑暗中小明从他的一大串钥匙中，随便选择一把，用它开门，下列叙述正确的是( )
A. 能开门的可能性大于不能开门的可能性 B. 不能开门的可能性大于能开门的可能性
C. 能开门的可能性与不能开门的可能性相等 D. 无法确定
B
【解析】既然是一大串钥匙，那么应该多于3把，而其中只有一把是能够开锁的，因此任取一把，不能开门的可能性大于能开门的可能性，故选B． 计算：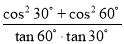 
+sin45°．
【解析】
试题分析：根据特殊角的三角函数值，可得实数的运算，根据实数的运算，可得答案．
试题解析：+sin45°
=
=2+
= 如图，某水库堤坝横断面迎水坡AB的坡比是1: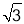
，堤坝高BC=50m，则迎水坡面AB的长度是（ ）.
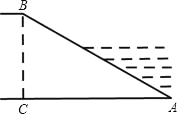
A．100m B．100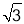m C．150m D．50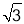m
A．
【解析】
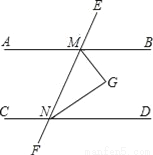
试题分析：根据题意可得，把BC=50m，代入即可算出AC的长，再利用勾股定理算出AB的长即可．∵堤坝横断面迎水坡AB的坡比是1: ，∴，∵BC=50m，∴AC=50m，∴AB==100m，故选：A． 如图，AB∥CD，∠BMN与∠DNM的平分线相交于点G．
（1）完成下面的证明：
∵MG平分∠BMN
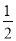∴∠GMN=
∠BMN
同理∠G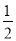NM=
∠DNM．
∵AB∥CD ，
∴∠BMN+∠DNM=
∴∠GMN+∠GNM=
∵∠GMN+∠GNM+∠G=
∴∠G=
∴MG与NG的位置关系是
（2）把上面的题设和结论，用文字语言概括为一个命题： ．
已知；角平分线的定义；已知；180°；90°；180°；90°；MG⊥NG.
【解析】试题分析：（1）根据平行线的性质进行填空即可；
（2）根据的特点作出结论．
试题解析：（1）∵MG平分∠BMN(已知)
(角平分线的定义)，
同理
∵ABCD(已知)，
∴MG与NG的位置关系是MG⊥NG；
故答案为：已知;角平分线的定义;已知; MG⊥NG；
(... 若三角形三个内角度数的比为2：3：4，则相应的外角比是__．
7：6：5
【解析】试题分析：由三角形的内角和是180°，三个内角的度数的比为2：3：4，可求得三个内角分别为40°，
60°，80°；从而对应的三个外角分别为140°，120°，100°；即可求得相应的的外角比. 若等腰三角形的一边是7，另一边是4，则此等腰三角形的周长是（ ）.
A．18 B．15 C．18或15 D．无法确定
C.
【解析】
试题分析：分情况讨论，假设7作腰长，则三边分别为7，7，4，周长为18；假设4作腰长，则三边分别为4，4，7，周长为15，所以此等腰三角形的周长是18或15.
故选：C. 从分别标有1、2、3、4的四张卡片中，一次同时抽2张，其中和为奇数的概率是 ．
【解析】试题分析：如图所示，
由树状图可知共有4×3=12种可能，和为奇数的有8种，所以概率是＝．故答案为： ．