题目内容
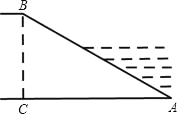
如图,某水库堤坝横断面迎水坡AB的坡比是1: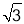 ,堤坝高BC=50m,则迎水坡面AB的长度是( ).
,堤坝高BC=50m,则迎水坡面AB的长度是( ).
A.100m B.100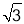 m C.150m D.50
m C.150m D.50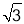 m
m
 A.
【解析】
试题分析:根据题意可得,把BC=50m,代入即可算出AC的长,再利用勾股定理算出AB的长即可.∵堤坝横断面迎水坡AB的坡比是1: ,∴,∵BC=50m,∴AC=50m,∴AB==100m,故选:A.
A.
【解析】
试题分析:根据题意可得,把BC=50m,代入即可算出AC的长,再利用勾股定理算出AB的长即可.∵堤坝横断面迎水坡AB的坡比是1: ,∴,∵BC=50m,∴AC=50m,∴AB==100m,故选:A.
练习册系列答案
相关题目
下列方程中,解为x=-3的方程是( )
A. 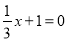 B. 2x-1=8-x C. -3x=1 D
B. 2x-1=8-x C. -3x=1 D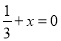
 A
【解析】试题分析:A、把x=-3代入方程x+1=0得:左边=0,右边=0,
左边=右边,
所以x=-3是方程的解,故本选项符合题意;
B、把x=-3代入方程2x-1=8-x得:左边=-7,右边=11,
左边≠右边,
所以x=-3不是方程的解,故本选项不符合题意;
C、把x=-3代入方程-3x=1得:左边=9,右边=1,
左边≠右边,
所以x...
A
【解析】试题分析:A、把x=-3代入方程x+1=0得:左边=0,右边=0,
左边=右边,
所以x=-3是方程的解,故本选项符合题意;
B、把x=-3代入方程2x-1=8-x得:左边=-7,右边=11,
左边≠右边,
所以x=-3不是方程的解,故本选项不符合题意;
C、把x=-3代入方程-3x=1得:左边=9,右边=1,
左边≠右边,
所以x... 用1、2、3三个数字组成一个三位数,则组成的数是偶数的概率是( )
A. 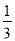 B.
B. 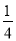 C.
C. 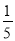 D.
D. 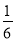
 A
【解析】用1,2,3三个数字组成一个三位数的所有组合是:123,132,213,231,312,321,是偶数只有2个,所以组成的三位数是偶数的概率是 ;
故选A。
A
【解析】用1,2,3三个数字组成一个三位数的所有组合是:123,132,213,231,312,321,是偶数只有2个,所以组成的三位数是偶数的概率是 ;
故选A。 如图,在一次数学课外实践活动中,要求测教学楼的高度AB、小刚在D处用高1.5m的测角仪CD,测得教学楼顶端A的仰角为30°,然后向教学楼前进40m到达E,又测得教学楼顶端A的仰角为60°.求这幢教学楼的高度AB.
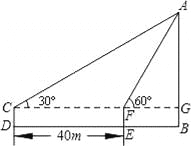
 米
【解析】试题分析:首先根据Rt△AFG中∠AFG的正切值得出FG的长度,然后根据∠ACG的正切得出CG的长度,然后根据CG-FG=40得出AG的长度,从而得出AB的长度.
试题解析:在Rt△AFG中,tan∠AFG=∴FG=
在Rt△ACG中, tan∠ACG=∴CG=又CG-FG=40
即AG-=40 ∴AG=20∴AB=20+1.5
答:这幢教学楼的高度AB为...
米
【解析】试题分析:首先根据Rt△AFG中∠AFG的正切值得出FG的长度,然后根据∠ACG的正切得出CG的长度,然后根据CG-FG=40得出AG的长度,从而得出AB的长度.
试题解析:在Rt△AFG中,tan∠AFG=∴FG=
在Rt△ACG中, tan∠ACG=∴CG=又CG-FG=40
即AG-=40 ∴AG=20∴AB=20+1.5
答:这幢教学楼的高度AB为... 已知在Rt△ABC中,∠C=90°,AC=4,cotA=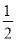 ,则BC的长是 .
,则BC的长是 .
 8
【解析】
试题分析:如图所示:
∵在Rt△ABC中,∠C=90°,AC=4,cotA=,
∴cotA==,
∴BC=8.
8
【解析】
试题分析:如图所示:
∵在Rt△ABC中,∠C=90°,AC=4,cotA=,
∴cotA==,
∴BC=8. 在直角三角形中,各边的长度都扩大3倍,则锐角A的三角函数值
A. 也扩大3倍 B. 缩小为原来的
C. 都不变 D. 有的扩大,有的缩小
 C
【解析】试题分析:根据锐角三角函数的概念,可知在直角三角形中,各边的长度都扩大3倍,锐角A的三角函数值不变.
故选C.
C
【解析】试题分析:根据锐角三角函数的概念,可知在直角三角形中,各边的长度都扩大3倍,锐角A的三角函数值不变.
故选C. 一个飞机零件的形状如图5—19所示,按规定∠A应等于90°,∠B,∠D应分别是20°和30°,康师傅量得∠BCD=143°,就能断定这个零件不合格,你能说出其中的道理吗?
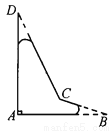
 不合格,理由见解析.
【解析】试题分析:延长BC与AD相交于点E,根据三角形的一个外角等于与它不相邻的两个内角的和求出∠BCD即可判断.
试题解析:如图,延长BC与AD相交于点E,
∵∠1是△ABE的外角,
同理,
∵李师傅量得不是
∴这个零件不合格.
不合格,理由见解析.
【解析】试题分析:延长BC与AD相交于点E,根据三角形的一个外角等于与它不相邻的两个内角的和求出∠BCD即可判断.
试题解析:如图,延长BC与AD相交于点E,
∵∠1是△ABE的外角,
同理,
∵李师傅量得不是
∴这个零件不合格. 三角形一个外角小于与它相邻的内角,这个三角形( )
A. 是直角三角形 B. 是锐角三角形
C. 是钝角三角形 D. 属于哪一类不能确定
 C
【解析】试题分析:锐角三角形的三个外角都大于与它相邻的内角;直角三角形的两个锐角的外角大于与它相邻的内角,直角的外角等于与它相邻的内角;钝角三角形的两个锐角的外角大于与它相邻的内角,钝角的外角小于与它相邻的内角.
C
【解析】试题分析:锐角三角形的三个外角都大于与它相邻的内角;直角三角形的两个锐角的外角大于与它相邻的内角,直角的外角等于与它相邻的内角;钝角三角形的两个锐角的外角大于与它相邻的内角,钝角的外角小于与它相邻的内角. 暑假将至,某商场为了吸引顾客,设计了可以自由转动的转盘(如图所示,转盘被均匀地分为20份),并规定:顾客每 200元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得200元、100元、50元的购物券,凭购物券可以在该商场继续购物.若某顾客购物300元.
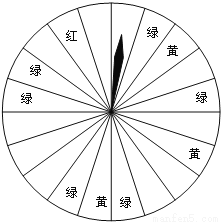
(1)求他此时获得购物券的概率是多少?
(2)他获得哪种购物券的概率最大?请说明理由.
 (1);(2)获得50元购物券的概率最大.
【解析】
试题分析:(1)由转盘被均匀地分为20份,他此时获得购物券的有10份,直接利用概率公式求解即可求得答案;
(2)分别求得获得200元、100元、50元的购物券的概率,即可求得答案.
【解析】
(1)∵转盘被均匀地分为20份,他此时获得购物券的有10份,
∴他此时获得购物券的概率是:=;
(2)∵P(获得20...
(1);(2)获得50元购物券的概率最大.
【解析】
试题分析:(1)由转盘被均匀地分为20份,他此时获得购物券的有10份,直接利用概率公式求解即可求得答案;
(2)分别求得获得200元、100元、50元的购物券的概率,即可求得答案.
【解析】
(1)∵转盘被均匀地分为20份,他此时获得购物券的有10份,
∴他此时获得购物券的概率是:=;
(2)∵P(获得20... 
