题目内容
多项式4n-2n2+2+6n2减去3（n2+2n3-1+3n）（n为自然数）的差一定是（ ）
| A、奇数 | B、偶数 |
| C、5的倍数 | D、以上答案都不对 |
考点：整式的加减
专题：
分析：先把4n-2n2+2+6n3-3（n2+2n3-1+3n）去括号，然后合并同类项得到-5n-5n2+5，即化简的结果为5（-n-n2+1），于是可判断差为5的倍数．
解答：解：4n-2n2+2+6n3-3（n2+2n3-1+3n）
=4n-2n2+2+6n3-3n2-6n3+3-9n
=-5n-5n2+5
=5（-n-n2+1）．
故选C．
=4n-2n2+2+6n3-3n2-6n3+3-9n
=-5n-5n2+5
=5（-n-n2+1）．
故选C．
点评：本题考查了整式的加减：几个整式相加减，通常用括号把每一个整式括起来，再用加减号连接；然后去括号、合并同类项．整式的加减实质上就是合并同类项．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
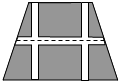如图，要设计一个等腰梯形的花坛，花坛上底长120米，下底长180米，上下底相距80米，在两腰中点连线（虚线）处有一条横向甬道，上下底之间有两条纵向甬道，各甬道的宽度相等．设甬道的宽为x米．
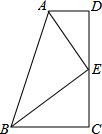如图，已知四边形ABCD中，∠D=∠C=90°，AE平分∠BAD，点E是DC的中点，且E在DC上．