题目内容
若关于x的不等式3x+1<m的正整数解是1,2,3,则整数m的最大值是 .
考点:一元一次不等式的整数解
专题:
分析:先解不等式得到x<
(m-1),再根据正整数解是1,2,3得到3<
(m-1)≤4时,然后从不等式的解集中找出适合条件的最大整数即可.
| 1 |
| 3 |
| 1 |
| 3 |
解答:解:解不等式3x+1<m,得x<
(m-1).
∵关于x的不等式3x+1<m的正整数解是1,2,3,
∴3<
(m-1)≤4,
∴10<m≤13,
∴整数m的最大值是13.
故答案为13.
| 1 |
| 3 |
∵关于x的不等式3x+1<m的正整数解是1,2,3,
∴3<
| 1 |
| 3 |
∴10<m≤13,
∴整数m的最大值是13.
故答案为13.
点评:本题考查了一元一次不等式的整数解:解决此类问题的关键在于正确解得不等式的解集,然后再根据题目中对于解集的限制得到下一步所需要的条件,再根据得到的条件进而求得不等式的最大整数解.

练习册系列答案
相关题目
多项式4n-2n2+2+6n2减去3(n2+2n3-1+3n)(n为自然数)的差一定是( )
| A、奇数 | B、偶数 |
| C、5的倍数 | D、以上答案都不对 |
 两圆的位置关系有多种.图中不存在的位置关系是
两圆的位置关系有多种.图中不存在的位置关系是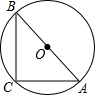 如图,AB是⊙O的直径,AC=BC,则∠A=
如图,AB是⊙O的直径,AC=BC,则∠A= 如图所示,AB为⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于点E,已知AB=2DE,∠AEC=20°.求∠AOC的度数.
如图所示,AB为⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于点E,已知AB=2DE,∠AEC=20°.求∠AOC的度数.