题目内容
问题:
已知方程x2+x-1=0,求一个一元二次方程,使它的根分别是已知方程根的2倍.
解:设所求方程的根为y,则y=2x,所以x=
.
把x=
代入已知方程,得(
)2+
-1=0.
化简,得:y2+2y-4=0.
这种利用方程根的代替求新方程的方法,我们成为“换根法”,请用阅读材料提供的“换根法”求新方程(要求:把所求方程化成一般形式);
(1)已知方程x2+x-2=0,求一个一元二次方程,使它的根分别是已知方程根的相反数.
(2)已知关于x的一元二次方程ax2+bx+c=0(a≠0)有两个不等于零的实数根,求一个一元二次方程,使它的根分别是已知方程根的倒数.
已知方程x2+x-1=0,求一个一元二次方程,使它的根分别是已知方程根的2倍.
解:设所求方程的根为y,则y=2x,所以x=
| y |
| 2 |
把x=
| y |
| 2 |
| y |
| 2 |
| y |
| 2 |
化简,得:y2+2y-4=0.
这种利用方程根的代替求新方程的方法,我们成为“换根法”,请用阅读材料提供的“换根法”求新方程(要求:把所求方程化成一般形式);
(1)已知方程x2+x-2=0,求一个一元二次方程,使它的根分别是已知方程根的相反数.
(2)已知关于x的一元二次方程ax2+bx+c=0(a≠0)有两个不等于零的实数根,求一个一元二次方程,使它的根分别是已知方程根的倒数.
考点:一元二次方程的解
专题:阅读型
分析:(1)设所求方程的根为y,则y=-x,则x=-y.将其代入已知方程,然后将其转化为一般形式即可;
(2)设所求方程的根为y,则y=
,将其代入已知方程,然后将其转化为一般形式即可.
(2)设所求方程的根为y,则y=
| 1 |
| x |
解答:解:(1)设所求方程的根为y,则y=-x,则x=-y.
把x=-y代入已知方程x2+x-2=0,
得 (-y)2+(-y)-2=0.
化简,得:y2-y-2=0.
(2)设所求方程的根为y,则y=
,所以x=
把x=
代入已知方程ax2+bx+c=0(a≠0)得
a(
)2+b•
+c=0,
去分母,得 a+by+cy2=0.
若c=0,则ax2+bx=0,于是方程ax2+bx+c=0(a≠0)有一根为0,不符合题意.
∴c≠0,故所求的方程为:cy2+by+c=0(c≠0).
把x=-y代入已知方程x2+x-2=0,
得 (-y)2+(-y)-2=0.
化简,得:y2-y-2=0.
(2)设所求方程的根为y,则y=
| 1 |
| x |
| 1 |
| y |
把x=
| 1 |
| y |
a(
| 1 |
| y |
| 1 |
| y |
去分母,得 a+by+cy2=0.
若c=0,则ax2+bx=0,于是方程ax2+bx+c=0(a≠0)有一根为0,不符合题意.
∴c≠0,故所求的方程为:cy2+by+c=0(c≠0).
点评:本题考查了一元二次方程的解.解答该题的关键是弄清楚“换根法”的具体解题方法.

练习册系列答案
相关题目
多项式4n-2n2+2+6n2减去3(n2+2n3-1+3n)(n为自然数)的差一定是( )
| A、奇数 | B、偶数 |
| C、5的倍数 | D、以上答案都不对 |
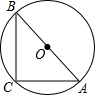 如图,AB是⊙O的直径,AC=BC,则∠A=
如图,AB是⊙O的直径,AC=BC,则∠A= 如图所示,⊙O的直径AB长为6,弦AC长为2,∠ACB的平分线交⊙O于点D.
如图所示,⊙O的直径AB长为6,弦AC长为2,∠ACB的平分线交⊙O于点D.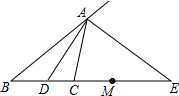 已知:AD、AE分别是△ABC的内外角平分线,M为DE中点,求证:
已知:AD、AE分别是△ABC的内外角平分线,M为DE中点,求证: