题目内容
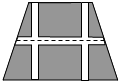 如图,要设计一个等腰梯形的花坛,花坛上底长120米,下底长180米,上下底相距80米,在两腰中点连线(虚线)处有一条横向甬道,上下底之间有两条纵向甬道,各甬道的宽度相等.设甬道的宽为x米.
如图,要设计一个等腰梯形的花坛,花坛上底长120米,下底长180米,上下底相距80米,在两腰中点连线(虚线)处有一条横向甬道,上下底之间有两条纵向甬道,各甬道的宽度相等.设甬道的宽为x米.(1)用含x的式子表示横向甬道的面积;
(2)当三条道的面积是梯形面积的八分之一时,求甬道的宽.
考点:一元二次方程的应用
专题:几何图形问题
分析:(1)甬道的形状是梯形,所以根据梯形面积公式即可求解;
(2)用含x的代数式表示出三条甬道的总面积,然后求出梯形的总面积,根据三条通道的面积是梯形面积的八分之一列方程求解,在求解过程中要注意三条甬道有重合部分.
(2)用含x的代数式表示出三条甬道的总面积,然后求出梯形的总面积,根据三条通道的面积是梯形面积的八分之一列方程求解,在求解过程中要注意三条甬道有重合部分.
解答:解:(1)横向甬道的面积为:(120+180)÷2×x=150x(m2);
(2)依题意:2×80×x+150x-2x2=
×(120+180)÷2×80,
整理得:x2-155x+750=0,
x1=5,x2=150(不符合题意,舍去),
答:甬道的宽为5米.
(2)依题意:2×80×x+150x-2x2=
| 1 |
| 8 |
整理得:x2-155x+750=0,
x1=5,x2=150(不符合题意,舍去),
答:甬道的宽为5米.
点评:考查一元二次方程的应用,得到甬道的总面积是解决本题的易错点.注意两个梯形的中位线是同一条.

练习册系列答案
相关题目
 如图是由一些相同的小正方体构成的立体图形分别从正面、左面、上面看到的形状图.那么构成这个立体图形的小正方体有( )
如图是由一些相同的小正方体构成的立体图形分别从正面、左面、上面看到的形状图.那么构成这个立体图形的小正方体有( )| A、4个 | B、5个 | C、6个 | D、7个 |
已知一棵树的影长是20m,同一时刻一根长1.5m竖直放立的标杆的影长为3m,则这棵树的高度是( )
| A、4.8m | B、6.4m |
| C、8m | D、10m |
在
,3.14,0.3131131113,π,
,1.
,-
,
中无理数的个数有( )
| 4 |
| 10 |
| •• |
| 51 |
| 0.001 |
| 2 |
| 7 |
| A、2个 | B、3个 | C、4个 | D、5个 |
多项式4n-2n2+2+6n2减去3(n2+2n3-1+3n)(n为自然数)的差一定是( )
| A、奇数 | B、偶数 |
| C、5的倍数 | D、以上答案都不对 |
 两圆的位置关系有多种.图中不存在的位置关系是
两圆的位置关系有多种.图中不存在的位置关系是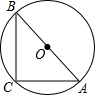 如图,AB是⊙O的直径,AC=BC,则∠A=
如图,AB是⊙O的直径,AC=BC,则∠A=