题目内容
2.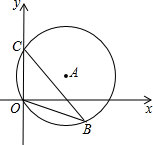 如图,直径为10的⊙A上经过点C(0,5)和点0(0,0),B是y轴右侧⊙A优弧上一点,则∠OBC的余弦值为( )
如图,直径为10的⊙A上经过点C(0,5)和点0(0,0),B是y轴右侧⊙A优弧上一点,则∠OBC的余弦值为( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{4}{5}$ |
分析 首先根据圆周角定理,判断出∠OBC=∠ODC;然后根据CD是⊙A的直径,判断出∠COD=90°,在Rt△COD中,用OD的长度除以CD的长度,求出∠ODC的余弦值为多少,进而判断出∠OBC的余弦值为多少即可.
解答 解:如图,延长CA交⊙A与点D,连接OD, ,
,
∵同弧所对的圆周角相等,
∴∠OBC=∠ODC,
∵CD是⊙A的直径,
∴∠COD=90°,
∴cos∠ODC=$\frac{OD}{CD}=\frac{\sqrt{{10}^{2}{-5}^{2}}}{10}$=$\frac{5\sqrt{3}}{10}$=$\frac{\sqrt{3}}{2}$,
∴cos∠OBC=$\frac{\sqrt{3}}{2}$,
即∠OBC的余弦值为$\frac{\sqrt{3}}{2}$.
故选:C.
点评 (1)此题主要考查了圆周角定理的应用,要熟练掌握,解答此题的关键是要明确:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
(2)此题还考查了特殊角的三角函数值的求法,要熟练掌握.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
17.甲、乙两组数据(单位:厘米)如下表
(1)根据以上数据填表(参考公式:S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2])
(2)那一组数据比较稳定?
| 甲组 | 173 | 172 | 174 | 172 | 174 |
| 乙组 | 173 | 174 | 172 | 173 | 173 |
| 众数(单位:厘米) | 平均数(单位:厘米) | 方差(单位:厘米) | |
| 甲组 | 172 | 173 | 0.8 |
| 乙组 | 173 | 173 | 0.4 |
7.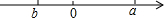 若实数a、b在数轴上的位置如图所示,则代数式|b-a|+$\sqrt{{a}^{2}}$化简为( )
若实数a、b在数轴上的位置如图所示,则代数式|b-a|+$\sqrt{{a}^{2}}$化简为( )
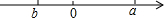 若实数a、b在数轴上的位置如图所示,则代数式|b-a|+$\sqrt{{a}^{2}}$化简为( )
若实数a、b在数轴上的位置如图所示,则代数式|b-a|+$\sqrt{{a}^{2}}$化简为( )| A. | b | B. | b-2a | C. | 2a-b | D. | b+2a |
11. 如图,在?ABCD中,BC=10,sinB=$\frac{9}{10}$,AC=BC,则?ABCD的面积是( )
如图,在?ABCD中,BC=10,sinB=$\frac{9}{10}$,AC=BC,则?ABCD的面积是( )
 如图,在?ABCD中,BC=10,sinB=$\frac{9}{10}$,AC=BC,则?ABCD的面积是( )
如图,在?ABCD中,BC=10,sinB=$\frac{9}{10}$,AC=BC,则?ABCD的面积是( )| A. | 2$\sqrt{19}$ | B. | 6$\sqrt{19}$ | C. | 9$\sqrt{19}$ | D. | 18$\sqrt{19}$ |
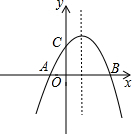 如图,已知二次函数y=-(x+1)(x-m)的图象与x轴相交于点A、B(点A在点B的左侧),与y轴相交于点C,且图象经过点M(2,3).
如图,已知二次函数y=-(x+1)(x-m)的图象与x轴相交于点A、B(点A在点B的左侧),与y轴相交于点C,且图象经过点M(2,3). 如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为2m,台阶AC的坡度为1:$\sqrt{3}$,且B、C、E三点在同一条直线上.请根据以上条件:
如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为2m,台阶AC的坡度为1:$\sqrt{3}$,且B、C、E三点在同一条直线上.请根据以上条件: 如图:把一个矩形如图折叠,使顶点B和D重合,折痕为EF.
如图:把一个矩形如图折叠,使顶点B和D重合,折痕为EF.