题目内容
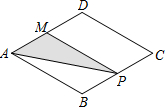 如图,菱形ABCD中,AB=2,∠B=120°,点M是AD的中点,点P由点A出发,沿A→B→C→D作匀速运动,到达点D停止,则△APM的面积y与点P经过的路程x之间的函数关系的图象大致是( )
如图,菱形ABCD中,AB=2,∠B=120°,点M是AD的中点,点P由点A出发,沿A→B→C→D作匀速运动,到达点D停止,则△APM的面积y与点P经过的路程x之间的函数关系的图象大致是( )A、 |
B、 |
C、 |
D、 |
考点:动点问题的函数图象
专题:数形结合
分析:分类讨论:当0≤x≤2,如图1,作PH⊥AD于H,AP=x,根据菱形的性质得∠A=60°,AM=1,则∠APH=30°,根据含30度的直角三角形三边的关系得到在RtAH=
x,PH=
x,然后根据三角形面积公式得y=
AM•PH=
x;当2<x≤4,如图2,作BE⊥AD于E,AP+BP=x,根据菱形的性质得∠A=60°,AM=2,AB=2,BC∥AD,则∠ABE=30°,在Rt△ABE中,根据含30度的直角三角形三边的关系得AE=1,PH=
,然后根据三角形面积公式得y=
AM•BE=
;
当4<x≤6,如图3,作PF⊥AD于F,AB+BC+PC=x,则PD=6-x,根据菱形的性质得∠ADC=120°,则∠DPF=30°,在Rt△DPF中,根据含30度的直角三角形三边的关系得DF=
(6-x),PF=
DF=
(6-x),则利用三角形面积公式得y=
AM•PF=-
x+3
,最后根据三个解析式和对应的取值范围对各选项进行判断.
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
当4<x≤6,如图3,作PF⊥AD于F,AB+BC+PC=x,则PD=6-x,根据菱形的性质得∠ADC=120°,则∠DPF=30°,在Rt△DPF中,根据含30度的直角三角形三边的关系得DF=
| 1 |
| 2 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
解答: 解:当点P在AB上运动时,即0≤x≤2,如图1,
解:当点P在AB上运动时,即0≤x≤2,如图1,
作PH⊥AD于H,AP=x,
∵菱形ABCD中,AB=2,∠B=120°,点M是AD的中点,
∴∠A=60°,AM=1,
∴∠APH=30°,
在Rt△APH中,AH=
AP=
x,
PH=
AH=
x,
∴y=
AM•PH=
•2•
x=
x;
当点P在BC上运动时,即2<x≤4,如图2,
作BE⊥AD于E,AP+BP=x,
∵四边形ABCD为菱形,∠B=120°,
∴∠A=60°,AM=2,AB=2,BC∥AD,
∴∠ABE=30°,
在Rt△ABE中,AE=
AB=1,
PH=
AE=
,
∴y=
AM•BE=
•2•
=
;
当点P在CD上运动时,即4<x≤6,如图3,
作PF⊥AD于F,AB+BC+PC=x,则PD=6-x,
∵菱形ABCD中,∠B=120°,
∴∠ADC=120°,
∴∠DPF=30°,
在Rt△DPF中,DF=
DP=
(6-x),
PF=
DF=
(6-x),
∴y=
AM•PF=
•2•
(6-x)=
(6-x)=-
x+3
,
∴△APM的面积y与点P经过的路程x之间的函数关系的图象为三段:当0≤x≤2,图象为线段,满足解析式y=
x;当2≤x≤4,图象为平行于x轴的线段,且到x轴的距离为
;当4≤x≤6,图象为线段,且满足解析式y=-
x+3
.
故选A.
 解:当点P在AB上运动时,即0≤x≤2,如图1,
解:当点P在AB上运动时,即0≤x≤2,如图1,作PH⊥AD于H,AP=x,
∵菱形ABCD中,AB=2,∠B=120°,点M是AD的中点,
∴∠A=60°,AM=1,
∴∠APH=30°,
在Rt△APH中,AH=
| 1 |
| 2 |
| 1 |
| 2 |
PH=
| 3 |
| ||
| 2 |
∴y=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |

当点P在BC上运动时,即2<x≤4,如图2,
作BE⊥AD于E,AP+BP=x,
∵四边形ABCD为菱形,∠B=120°,
∴∠A=60°,AM=2,AB=2,BC∥AD,
∴∠ABE=30°,
在Rt△ABE中,AE=
| 1 |
| 2 |
PH=
| 3 |
| 3 |
∴y=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
当点P在CD上运动时,即4<x≤6,如图3,

作PF⊥AD于F,AB+BC+PC=x,则PD=6-x,
∵菱形ABCD中,∠B=120°,
∴∠ADC=120°,
∴∠DPF=30°,
在Rt△DPF中,DF=
| 1 |
| 2 |
| 1 |
| 2 |
PF=
| 3 |
| ||
| 2 |
∴y=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 3 |
∴△APM的面积y与点P经过的路程x之间的函数关系的图象为三段:当0≤x≤2,图象为线段,满足解析式y=
| ||
| 2 |
| 3 |
| ||
| 2 |
| 3 |
故选A.
点评:本题考查了动点问题的函数图象:利用点运动的几何性质列出有关的函数关系式,然后根据函数关系式画出函数图象,注意自变量的取值范围.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
下列说法中,正确的是( )
| A、a一定是正数 | ||
| B、没有绝对值最小的实数 | ||
C、2
| ||
D、
|
若
是二元一次方程组
的解,则
的值是( )
|
|
| n |
| m |
| A、-5 | ||
B、-
| ||
| C、-10 | ||
D、-
|
 如图,一条公路修到湖边时,需拐弯绕湖而过,第一次拐的角∠A=110°,第二次拐的角∠B=150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C的度数为( )
如图,一条公路修到湖边时,需拐弯绕湖而过,第一次拐的角∠A=110°,第二次拐的角∠B=150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C的度数为( )| A、120° | B、130° |
| C、140° | D、150° |
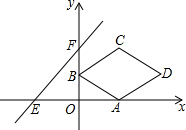 如图,在平面直角坐标系xOy中,菱形ABCD的顶点A的坐标为(2,0),点B的坐标为(0,1),点C在第一象限,对角线BD与x轴平行.直线y=x+3与x轴、y轴分别交于点E,F.将菱形ABCD沿x轴向左平移m个单位,当点D落在△EOF的内部时(不包括三角形的边),m的值可能是( )
如图,在平面直角坐标系xOy中,菱形ABCD的顶点A的坐标为(2,0),点B的坐标为(0,1),点C在第一象限,对角线BD与x轴平行.直线y=x+3与x轴、y轴分别交于点E,F.将菱形ABCD沿x轴向左平移m个单位,当点D落在△EOF的内部时(不包括三角形的边),m的值可能是( )
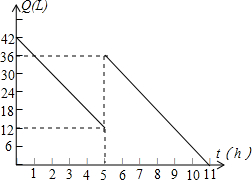 机动车出发前油箱内有油42升,行驶若干小时后,途中在加油站加油若干升,油箱中余油量Q(L)与行驶时间t(h)之间的关系如图所示,根据图回答问题.
机动车出发前油箱内有油42升,行驶若干小时后,途中在加油站加油若干升,油箱中余油量Q(L)与行驶时间t(h)之间的关系如图所示,根据图回答问题. 如图,在Rt△ABC中,∠ABC=90°,点F为AC中点,⊙O经过点B,F,且与AC交于点D,与AB交于点E,与BC交于点G,连结BF,DE,弧EFG的长度为(1+
如图,在Rt△ABC中,∠ABC=90°,点F为AC中点,⊙O经过点B,F,且与AC交于点D,与AB交于点E,与BC交于点G,连结BF,DE,弧EFG的长度为(1+