题目内容
 如图,在Rt△ABC中,∠ACB=90°,点D,E分别是边AB,AC的中点,延长BC到点F,使CF=
如图,在Rt△ABC中,∠ACB=90°,点D,E分别是边AB,AC的中点,延长BC到点F,使CF=| 1 |
| 2 |
考点:平行四边形的判定与性质,直角三角形斜边上的中线,三角形中位线定理
专题:压轴题
分析:根据三角形中位线的性质,可得DE与BC的关系,根据平行四边形的判定与性质,可得DC与EF的关系,根据直角三角形的性质,可得DC与AB的关系,可得答案.
解答: 解:如图,连接DC.
解:如图,连接DC.
DE是△ABC的中位线,
∴DE∥BC,DE=
BC,
∵CF=
BC,
∴DE∥CF,DE=CF,
∴CDEF是平行四边形,
∴EF=DC.
∵DC是Rt△ABC斜边上的中线,
∴DC=
AB=5,
∴EF=DC=5,
故答案为:5.
 解:如图,连接DC.
解:如图,连接DC.DE是△ABC的中位线,
∴DE∥BC,DE=
| 1 |
| 2 |
∵CF=
| 1 |
| 2 |
∴DE∥CF,DE=CF,
∴CDEF是平行四边形,
∴EF=DC.
∵DC是Rt△ABC斜边上的中线,
∴DC=
| 1 |
| 2 |
∴EF=DC=5,
故答案为:5.
点评:本题考查了平行四边形的判定与性质,利用了平行四边形的判定与性质,直角三角形斜边上的中线等于斜边的一半.

练习册系列答案
相关题目
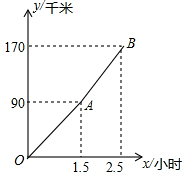 “五一节”期间,王老师一家自驾游去了离家170千米的某地,下面是他们家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象,当他们离目的地还有20千米时,汽车一共行驶的时间是( )
“五一节”期间,王老师一家自驾游去了离家170千米的某地,下面是他们家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象,当他们离目的地还有20千米时,汽车一共行驶的时间是( )| A、2小时 | B、2.2小时 |
| C、2.25小时 | D、2.4小时 |
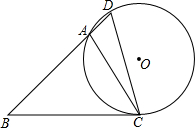 如图,在△ABC中,∠B=45°,∠ACB=60°,AB=3
如图,在△ABC中,∠B=45°,∠ACB=60°,AB=3 如图,F在BD上,BC、AD相交于点E,且AB∥CD∥EF,
如图,F在BD上,BC、AD相交于点E,且AB∥CD∥EF,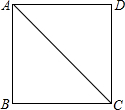 如图,在正方形ABCD中,对角线AC为2,则正方形边长为
如图,在正方形ABCD中,对角线AC为2,则正方形边长为