题目内容
(1)计算
-|2-tan60°|-(
-π)0+(-
)-2.
(2)解方程:
-
+
=0.
(3)已知关于x,y的方程组
的解都不大于1,求:
①m的范围.
②化简:
+
+|m+3|+|m-5|-|x+y-2|.
| 1 |
| 2 |
| 12 |
| 3 |
| 1 |
| 2 |
(2)解方程:
| x-1 |
| x+2 |
| 3(x+2) |
| 2(x-1) |
| 5 |
| 2 |
(3)已知关于x,y的方程组
|
①m的范围.
②化简:
| x2-2x+1 |
| y2-2y+1 |
考点:实数的运算,零指数幂,负整数指数幂,二次根式的性质与化简,二元一次方程组的解,解分式方程,特殊角的三角函数值
专题:
分析:(1)运用开平方、绝对值的意义、负整数指数幂和0次幂求解.
(2)方程两边同时乘2(x+2)(x-1)化为整式方程再求解,并验根.
(3)利用方程组求出m,利用不等式组求出m的取值范围.再运用开平方、绝对值的意义求解.
(2)方程两边同时乘2(x+2)(x-1)化为整式方程再求解,并验根.
(3)利用方程组求出m,利用不等式组求出m的取值范围.再运用开平方、绝对值的意义求解.
解答:解:(1)
-|2-tan60°|-(
-π)0+(-
)-2
=
-2+
-1+4
=2
+1;
(2)解方程:
-
+
=0,
方程两边同时乘2(x+2)(x-1)得
2(x-1)2-3(x+2)2+5(x+2)(x-1)=0,
化简得:4x2-11x-20=0,
解得:x1=4, x2=-
;
经检验x1=4, x2=-
是原方程的根;
(3)①解方程组得:
,
∵
,
∴
,
解得:-3≤m≤5;
②∵-3≤m≤5
∴
∵
+
+|m+3|+|m-5|-|x+y-2|
=1-x+1-y+m+3-m+5+x+y-2
=8.
| 1 |
| 2 |
| 12 |
| 3 |
| 1 |
| 2 |
=
| 3 |
| 3 |
=2
| 3 |
(2)解方程:
| x-1 |
| x+2 |
| 3(x+2) |
| 2(x-1) |
| 5 |
| 2 |
方程两边同时乘2(x+2)(x-1)得
2(x-1)2-3(x+2)2+5(x+2)(x-1)=0,
化简得:4x2-11x-20=0,
解得:x1=4, x2=-
| 5 |
| 4 |
经检验x1=4, x2=-
| 5 |
| 4 |
(3)①解方程组得:
|
∵
|
∴
|
解得:-3≤m≤5;
②∵-3≤m≤5
∴
|
∵
|
| x2-2x+1 |
| y2-2y+1 |
=1-x+1-y+m+3-m+5+x+y-2
=8.
点评:本题主要考查开平方、绝对值的意义、负整数指数幂和0次幂及解分式方程和运用不等式求m的范围.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
若a>b,则下列不等式中,不成立的是( )
| A、a+5>b+5 |
| B、a-5>b-5 |
| C、5a>5b |
| D、-5a>-5b |
 如图,在Rt△ABC中,∠ACB=90°,点D,E分别是边AB,AC的中点,延长BC到点F,使CF=
如图,在Rt△ABC中,∠ACB=90°,点D,E分别是边AB,AC的中点,延长BC到点F,使CF= 如图,在梯形AOBC中,AO∥CB,点A、B分别在y轴和x轴上.P是OB中点,以P为圆心,PB长为半径作半圆,D为该半圆与AC的一个公共点,且OB=CB=CD=4.
如图,在梯形AOBC中,AO∥CB,点A、B分别在y轴和x轴上.P是OB中点,以P为圆心,PB长为半径作半圆,D为该半圆与AC的一个公共点,且OB=CB=CD=4.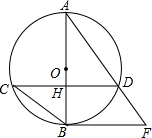 如图,AB为⊙O的直径,弦CD⊥AB于点H,过点B作⊙O的切线与AD的延长线交于F.
如图,AB为⊙O的直径,弦CD⊥AB于点H,过点B作⊙O的切线与AD的延长线交于F.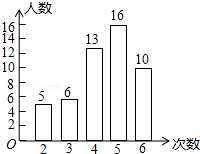 我市开展了“寻找雷锋足迹”的活动,某中学为了了解七年在“学雷锋活动月”中做好事的情况,随机调查了七年级50名学生在一个月内做好事的次数,并将所得数据绘制成统计图,请根据图中提供的信息解答下列问题:
我市开展了“寻找雷锋足迹”的活动,某中学为了了解七年在“学雷锋活动月”中做好事的情况,随机调查了七年级50名学生在一个月内做好事的次数,并将所得数据绘制成统计图,请根据图中提供的信息解答下列问题: