题目内容
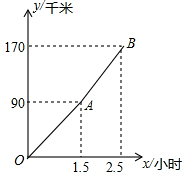 “五一节”期间,王老师一家自驾游去了离家170千米的某地,下面是他们家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象,当他们离目的地还有20千米时,汽车一共行驶的时间是( )
“五一节”期间,王老师一家自驾游去了离家170千米的某地,下面是他们家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象,当他们离目的地还有20千米时,汽车一共行驶的时间是( )| A、2小时 | B、2.2小时 |
| C、2.25小时 | D、2.4小时 |
考点:一次函数的应用
专题:数形结合
分析:根据待定系数法,可得一次函数解析式,根据函数值,可得相应自变量的值.
解答:解:设AB段的函数解析式是y=kx+b,
y=kx+b的图象过A(1.5,90),B(2.5,170),
,
解得
∴AB段函数的解析式是y=80x-30,
离目的地还有20千米时,即y=170-20=150km,
当y=150时,80x-30=150
解得:x=2.25h,
故选:C.
y=kx+b的图象过A(1.5,90),B(2.5,170),
|
解得
|
∴AB段函数的解析式是y=80x-30,
离目的地还有20千米时,即y=170-20=150km,
当y=150时,80x-30=150
解得:x=2.25h,
故选:C.
点评:本题考查了一次函数的应用,利用了待定系数法求解析式,利用函数值求自变量的值.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
 如图,函数y=kx(k≠0)和y=ax+4(a≠0)的图象相交于点A(2,3),则不等式kx>ax+4的解集为( )
如图,函数y=kx(k≠0)和y=ax+4(a≠0)的图象相交于点A(2,3),则不等式kx>ax+4的解集为( )| A、x>3 | B、x<3 |
| C、x>2 | D、x<2 |
分式方程
-1=
有增根,则m的值为( )
| x |
| x-1 |
| m |
| (x-1)(x+1) |
| A、0和2 | B、1 | C、1和-2 | D、2 |
若a>b,则下列不等式中,不成立的是( )
| A、a+5>b+5 |
| B、a-5>b-5 |
| C、5a>5b |
| D、-5a>-5b |
 如图,AD是△ABC的一条中线,若BD=5,则BC=
如图,AD是△ABC的一条中线,若BD=5,则BC= 如图,在Rt△ABC中,∠ACB=90°,点D,E分别是边AB,AC的中点,延长BC到点F,使CF=
如图,在Rt△ABC中,∠ACB=90°,点D,E分别是边AB,AC的中点,延长BC到点F,使CF=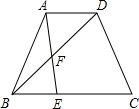 如图,等腰梯形ABCD中,AD∥BC,AD=1,BC=3,AB=CD=2,射线AB绕点A逆时针旋转分别与BD、BC交于点F、E,旋转角∠BAE=∠DBC,则BE=
如图,等腰梯形ABCD中,AD∥BC,AD=1,BC=3,AB=CD=2,射线AB绕点A逆时针旋转分别与BD、BC交于点F、E,旋转角∠BAE=∠DBC,则BE=