题目内容
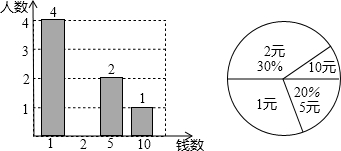
14.在“爱心一日捐”活动中,九年级1班50名学生全部参与.该班某小组对捐款情况绘制了如下不完整的两个统计图:根据以上统计图提供的信息,回答下列问题:(1)此小组学生人数为10人,其中捐款1元的学生人数占小组人数的百分比为40%;
(2)补全条形统计图;
(3)在扇形统计图中求“2元”部分的圆心角;
(4)甲乙丙丁四名同学捐款数额各不相同,在这四名同学中随机抽取两名,画树状图表示出所有可能抽到的结果,并求抽到的两名学生捐款数额超过10元的概率.
分析 (1)用捐款2元的人数除以其所占的百分比即可求得总人数;
(2)求得捐款2元的人数即可补全条形统计图;
(3)用周角乘以2元所占的百分比即可求得圆心角;
(4)列表将所有等可能的结果列举出来,利用概率公式求解即可.
解答 解:(1)捐款5元的有2人,占20%,
故总人数为2÷20%=10人;
$\frac{4}{10}$×100%=40%;
(2)条形统计图为:
(3)在扇形统计图中求“2元”部分的圆心角为30%×360°=108°;
(4)列树状图得:
故P(超过10元)=$\frac{6}{12}$=$\frac{1}{2}$.
点评 此题考查的是用树状图法求概率,树状图法适用于两步或两步以上完成的事件,解题时还要注意是放回实验还是不放回实验,用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
2.四名运动员参加了射击预选赛,他们成绩的平均环数$\overline{x}$及其方差s2如下表所示,
如果选出一个成绩较好且状态稳定的人去参赛,那么应选( )
| 甲 | 乙 | 丙 | 丁 | |
| $\overline{x}$ | 8.3 | 9.2 | 9.2 | 8.5 |
| s2 | 1 | 1 | 1.2 | 1.7 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
9.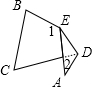 如图:把△ABC纸片沿DE折叠,当点A在四边形BCDE的外部时,记∠AEB为∠1,∠ADC为∠2,则∠A、∠1与∠2的数量关系,结论正确的是( )
如图:把△ABC纸片沿DE折叠,当点A在四边形BCDE的外部时,记∠AEB为∠1,∠ADC为∠2,则∠A、∠1与∠2的数量关系,结论正确的是( )
 如图:把△ABC纸片沿DE折叠,当点A在四边形BCDE的外部时,记∠AEB为∠1,∠ADC为∠2,则∠A、∠1与∠2的数量关系,结论正确的是( )
如图:把△ABC纸片沿DE折叠,当点A在四边形BCDE的外部时,记∠AEB为∠1,∠ADC为∠2,则∠A、∠1与∠2的数量关系,结论正确的是( )| A. | ∠1=∠2+∠A | B. | ∠1=2∠A+∠2 | C. | ∠1=2∠2+2∠A | D. | 2∠1=∠2+∠A |
19.下列不等式变形正确的是( )
| A. | 由4x-1≥0得4x>1 | B. | 由5x>3 得 x>3 | C. | 由$\frac{y}{2}$>0得 y>0 | D. | 由-2x<4得x<-2 |