题目内容
3. 如图,在平行四边形ABCD中,AB=10,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F恰好为DC的中点,DG⊥AE,垂足为G.若DG=3,则AE的边长为( )
如图,在平行四边形ABCD中,AB=10,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F恰好为DC的中点,DG⊥AE,垂足为G.若DG=3,则AE的边长为( )| A. | 2$\sqrt{3}$ | B. | 4 | C. | 8 | D. | 16 |
分析 由平行四边形的性质和角平分线证出AD=DF,由F为DC中点,AB=CD,求出AD与DF的长,得出三角形ADF为等腰三角形,根据三线合一得到G为AF中点,在直角三角形ADG中,由AD与DG的长,利用勾股定理求出AG的长,进而求出AF的长,再由AAS证明ADF≌△ECF全等,得出AF=EF,即可求出AE的长.
解答 解:∵AE为∠DAB的平分线,
∴∠DAE=∠BAE,
∵DC∥AB,
∴∠BAE=∠DFA,
∴∠DAE=∠DFA,
∴AD=FD,
又F为DC的中点,
∴DF=CF,
∴AD=DF=$\frac{1}{2}$DC=$\frac{1}{2}$AB=5,
在Rt△ADG中,根据勾股定理得:AG=$\sqrt{{5}^{2}-{3}^{2}}$=4,
则AF=2AG=8,
∵平行四边形ABCD中,
∴AD∥BC,
∴∠DAF=∠E,∠ADF=∠ECF,
在△ADF和△ECF中,$\left\{\begin{array}{l}{∠DAF=∠E}\\{∠ADF=∠ECF}\\{DF=CF}\end{array}\right.$,
∴△ADF≌△ECF(AAS),
∴AF=EF,
则AE=2AF=2×8=16.
故选D.
点评 此题考查了平行四边形的性质,全等三角形的判定与性质,勾股定理,等腰三角形的判定与性质;熟练掌握平行四边形的判定与性质,证明三角形全等是解本题的关键.

练习册系列答案
相关题目
14. 如图,边长为$\frac{5}{4}$的正方形ABCD的顶点A在y轴上,顶点D在反比例函数$y=\frac{k}{x}(x>0)$的图象上,已知点B的坐标是$({\frac{3}{4},\frac{9}{4}})$,则k的值为( )
如图,边长为$\frac{5}{4}$的正方形ABCD的顶点A在y轴上,顶点D在反比例函数$y=\frac{k}{x}(x>0)$的图象上,已知点B的坐标是$({\frac{3}{4},\frac{9}{4}})$,则k的值为( )
 如图,边长为$\frac{5}{4}$的正方形ABCD的顶点A在y轴上,顶点D在反比例函数$y=\frac{k}{x}(x>0)$的图象上,已知点B的坐标是$({\frac{3}{4},\frac{9}{4}})$,则k的值为( )
如图,边长为$\frac{5}{4}$的正方形ABCD的顶点A在y轴上,顶点D在反比例函数$y=\frac{k}{x}(x>0)$的图象上,已知点B的坐标是$({\frac{3}{4},\frac{9}{4}})$,则k的值为( )| A. | $\frac{27}{16}$ | B. | $\frac{27}{8}$ | C. | 4 | D. | 6 |
8.在△ABC中,(2cosA-$\sqrt{2}$)2+|1-tanB|=0,则△ABC一定是( )
| A. | 直角三角形 | B. | 等腰三角形 | C. | 等边三角形 | D. | 等腰直角三角形 |
13.一元二次方程x2-2x-1=0,其解的情况正确的是( )
| A. | 有两个相等的实数解 | B. | 有两个不相等的实数解 | ||
| C. | 没有实数解 | D. | 不确定 |
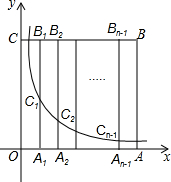 如图,边长为n(n为正整数)的正方形OABC的边OA、OC在坐标轴上,点A1,A2,…,An-1为OA的n等分点,点B1,B2,B3…,Bn-1为CB的n等分点,连接A1B1,A2B2,A3B3,…,An-1Bn-1,分别与曲线y=$\frac{n-8}{x}$(x>0)相交于点C1,C2,C3…,Cn-1.若B6C6=9A6C6,则n的值是20.
如图,边长为n(n为正整数)的正方形OABC的边OA、OC在坐标轴上,点A1,A2,…,An-1为OA的n等分点,点B1,B2,B3…,Bn-1为CB的n等分点,连接A1B1,A2B2,A3B3,…,An-1Bn-1,分别与曲线y=$\frac{n-8}{x}$(x>0)相交于点C1,C2,C3…,Cn-1.若B6C6=9A6C6,则n的值是20.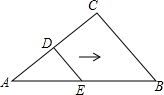 如图,D、E分别是AC和AB上的点,AD=DC=4,DE=3,DE∥BC,∠C=90°,将△ADE沿着AB边向右平移,当点D落在BC上时,平移的距离为( )
如图,D、E分别是AC和AB上的点,AD=DC=4,DE=3,DE∥BC,∠C=90°,将△ADE沿着AB边向右平移,当点D落在BC上时,平移的距离为( )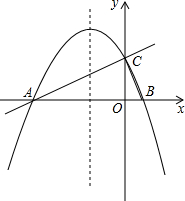 已知抛物线的解析式为y=-$\frac{1}{2}{x^2}-\frac{3}{2}$x+c.
已知抛物线的解析式为y=-$\frac{1}{2}{x^2}-\frac{3}{2}$x+c.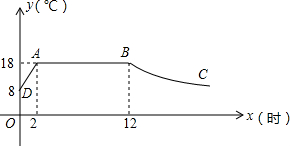 我市某蔬菜生产基地在气温较低时,用装有恒温系统的大鹏栽培一种在自然光照且温度为18℃的条件下生长最快的新品种,如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=$\frac{k}{x}$的一部分.请根据图中信息解析下列问题:
我市某蔬菜生产基地在气温较低时,用装有恒温系统的大鹏栽培一种在自然光照且温度为18℃的条件下生长最快的新品种,如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=$\frac{k}{x}$的一部分.请根据图中信息解析下列问题: