题目内容
13.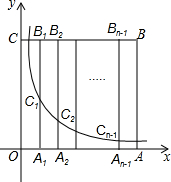 如图,边长为n(n为正整数)的正方形OABC的边OA、OC在坐标轴上,点A1,A2,…,An-1为OA的n等分点,点B1,B2,B3…,Bn-1为CB的n等分点,连接A1B1,A2B2,A3B3,…,An-1Bn-1,分别与曲线y=$\frac{n-8}{x}$(x>0)相交于点C1,C2,C3…,Cn-1.若B6C6=9A6C6,则n的值是20.
如图,边长为n(n为正整数)的正方形OABC的边OA、OC在坐标轴上,点A1,A2,…,An-1为OA的n等分点,点B1,B2,B3…,Bn-1为CB的n等分点,连接A1B1,A2B2,A3B3,…,An-1Bn-1,分别与曲线y=$\frac{n-8}{x}$(x>0)相交于点C1,C2,C3…,Cn-1.若B6C6=9A6C6,则n的值是20.
分析 先根据正方形OABC的边长为n,点A1,A2,…,An-1为OA的n等分点,点B1,B2,…,Bn-1为CB的n等分点可知OA6=n,A15B15=15,再根据B6C6=9A6C6表示出C6的坐标,代入反比例函数的解析式求出n的值.
解答 解:∵正方形OABC的边长为n,点A1,A2,…,An-1为OA的n等分点,点B1,B2,…,Bn-1为CB的n等分点,
∴OA6=6,A6B6=n,
∵B6C6=9A6C6,
∴C6(6,$\frac{n}{6}$),
∵点C6在曲线y=$\frac{n-8}{x}$(x>0)上,
∴6×$\frac{n}{6}$=n-8,
解得n=20.
故答案为:20.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上k=xy为定值是解答此题的关键.

练习册系列答案
相关题目
20.东方学校将为2013级新生购置课桌椅,从批发地运到学校有火车和汽车两种运输工具,运输过程中的损耗均为160元/时,其他主要参考数据如下:
(1)如果从批发地运到学校有400千米,请问汽车和火车的总支出费用各是多少?
(2)若两种运输工具的费用相等,你知道批发地到学校之间的路程是多少千米吗?请你用方程解答;
(3)如果从批发地到学校的距离为S,选择哪种运输工具比较合算呢?
| 运输工具 | 平均速度(千米/时) | 运费(元/千米) | 装卸费用(元) |
| 火车 | 100 | 18 | 1800 |
| 汽车 | 80 | 22 | 1000 |
(2)若两种运输工具的费用相等,你知道批发地到学校之间的路程是多少千米吗?请你用方程解答;
(3)如果从批发地到学校的距离为S,选择哪种运输工具比较合算呢?
5.若实数x、y满足$\sqrt{2x-1}+|{y-1}|=0$,则x+y的值是( )
| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | $\frac{5}{2}$ |
2.若a-b=3,ab=1,则a2+b2的值是( )
| A. | 5 | B. | 7 | C. | 9 | D. | 11 |
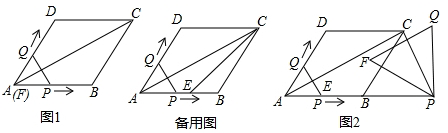
3. 如图,在平行四边形ABCD中,AB=10,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F恰好为DC的中点,DG⊥AE,垂足为G.若DG=3,则AE的边长为( )
如图,在平行四边形ABCD中,AB=10,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F恰好为DC的中点,DG⊥AE,垂足为G.若DG=3,则AE的边长为( )
 如图,在平行四边形ABCD中,AB=10,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F恰好为DC的中点,DG⊥AE,垂足为G.若DG=3,则AE的边长为( )
如图,在平行四边形ABCD中,AB=10,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F恰好为DC的中点,DG⊥AE,垂足为G.若DG=3,则AE的边长为( )| A. | 2$\sqrt{3}$ | B. | 4 | C. | 8 | D. | 16 |
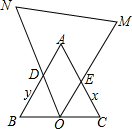 如图,△ABC、△OMN均为等边三角形,且O点为BC的中点,△OMN绕着点O旋转,ON、OM分别交BA(BA的延长线),CA(CA的延长线)于D、E两点.
如图,△ABC、△OMN均为等边三角形,且O点为BC的中点,△OMN绕着点O旋转,ON、OM分别交BA(BA的延长线),CA(CA的延长线)于D、E两点.