题目内容
11.已知△ABC中,∠C=90°,BC=1,AC=2,沿着某条直线翻折,使点A落在点B处,折痕与边AC交于点D,则CD的长度为$\frac{3}{4}$.分析 先根据题意画出图形,由翻折的性质可知:BD=DA.设DC=x,则DB=AD=2-x,在Rt△BCD中依据勾股定理列方程求解即可.
解答 解:如图所示:
由翻折的性质可知:BD=DA.
设DC=x,则DB=AD=2-x.
在Rt△BCD中,BC2+CD2=BD2,即12+x2=(2-x)2.
解得:x=$\frac{3}{4}$.
则CD=$\frac{3}{4}$.
故答案为:$\frac{3}{4}$.
点评 本题主要考查的是翻折的性质、勾股定理的应用,根据勾股定理列出关于x的方程是解题的关键.

练习册系列答案
相关题目
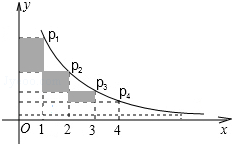 如图,在反比例函数y=$\frac{2}{x}$(x>0)的图象上,有点P1,P2,P3,…,P2010,它们的横坐标依次为1,2,3,…,2015.分别过这些点作
如图,在反比例函数y=$\frac{2}{x}$(x>0)的图象上,有点P1,P2,P3,…,P2010,它们的横坐标依次为1,2,3,…,2015.分别过这些点作