题目内容
1.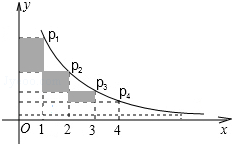 如图,在反比例函数y=$\frac{2}{x}$(x>0)的图象上,有点P1,P2,P3,…,P2010,它们的横坐标依次为1,2,3,…,2015.分别过这些点作
如图,在反比例函数y=$\frac{2}{x}$(x>0)的图象上,有点P1,P2,P3,…,P2010,它们的横坐标依次为1,2,3,…,2015.分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1,
S2,S3,…,S2010,则S1+S2+S3+…+S2015=$\frac{4030}{2016}$.
分析 求出P1、P2、P3、P4…的纵坐标,从而可计算出S1、S2、S3、S4…的高,进而求出S1、S2、S3、S4…,从而得出S1+S2+S3+…+Sn的值.
解答  解:当x=1时,P1的纵坐标为2,
解:当x=1时,P1的纵坐标为2,
当x=2时,P2的纵坐标1,
当x=3时,P3的纵坐标$\frac{2}{3}$,
当x=4时,P4的纵坐标$\frac{1}{2}$,
当x=5时,P5的纵坐标$\frac{2}{5}$,
…
则S1=1×(2-1)=2-1;
S2=1×(1-$\frac{2}{3}$)=1-$\frac{2}{3}$;
S3=1×($\frac{2}{3}$-$\frac{1}{2}$)=$\frac{2}{3}$-$\frac{2}{4}$;
S4=1×($\frac{1}{2}$-$\frac{2}{5}$)=$\frac{2}{4}$-$\frac{2}{5}$;
…
Sn=$\frac{2}{n}$-$\frac{2}{n+1}$;
S1+S2+S3+…+Sn=2-1+1-$\frac{2}{3}$+$\frac{2}{3}$-$\frac{2}{4}$+$\frac{2}{4}$-$\frac{2}{5}$+…+$\frac{2}{n}$-$\frac{2}{n}$=2-$\frac{2}{n+1}$=$\frac{2n}{n+1}$,
∴S1+S2+S3+…+S2015=$\frac{4030}{2016}$,
故答案为:$\frac{4030}{2016}$.
点评 此题考查了反比例函数图象上点的坐标特征,根据坐标求出个阴影的面积表达式是解题的关键.

练习册系列答案
相关题目
11.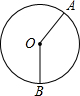 如图,圆中两条半径把圆分成面积为4:5的两个扇形,则两个扇形的圆心角的度数为( )
如图,圆中两条半径把圆分成面积为4:5的两个扇形,则两个扇形的圆心角的度数为( )
 如图,圆中两条半径把圆分成面积为4:5的两个扇形,则两个扇形的圆心角的度数为( )
如图,圆中两条半径把圆分成面积为4:5的两个扇形,则两个扇形的圆心角的度数为( )| A. | 40°和50° | B. | 80°和100° | C. | 120°和150° | D. | 160°和200° |
12.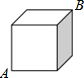 如图,已知正方体的棱长为1,则蚂蚁在表面上从一个顶点A爬行到相对顶点B的最短路程为( )
如图,已知正方体的棱长为1,则蚂蚁在表面上从一个顶点A爬行到相对顶点B的最短路程为( )
 如图,已知正方体的棱长为1,则蚂蚁在表面上从一个顶点A爬行到相对顶点B的最短路程为( )
如图,已知正方体的棱长为1,则蚂蚁在表面上从一个顶点A爬行到相对顶点B的最短路程为( )| A. | 3 | B. | $\sqrt{2}+1$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
 一个正方体的表面展开图如图所示,则原正方体中的“★”所在面的对面所标的字是田.
一个正方体的表面展开图如图所示,则原正方体中的“★”所在面的对面所标的字是田.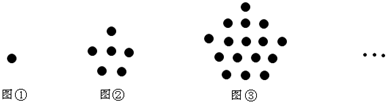
 画图题
画图题 如图:在△ABC中,AB=7,AC=5,AD是它的角平分线,则S△ABD:S△ACD=$\frac{7}{5}$.
如图:在△ABC中,AB=7,AC=5,AD是它的角平分线,则S△ABD:S△ACD=$\frac{7}{5}$.