题目内容
17．在平面直角坐标系中，点P（a，3）与点Q（-2，b）关于原点成中心对称，则a+b的值为（ ）| A． | -5 | B． | -1 | C． | 1 | D． | 5 |
分析 首先根据点P（a，3）与点Q（-2，b）关于原点成中心对称，可得a=2，b=-3，然后把a、b的值代入，求出a+b的值为多少即可．
解答 解：∵点P（a，3）与点Q（-2，b）关于原点成中心对称，
∴a=2，b=-3，
∴a+b=2-3=-1．
故选：B．
点评 此题主要考查了关于原点对称的点的坐标，要熟练掌握，解答此题的关键是要明确：两个点关于原点对称时，它们的坐标符号相反，即点P（x，y）关于原点O的对称点是P′（-x，-y）．
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
7．掷一枚质地均匀的正方体骰子，骰子的六个面上分别标有1、2、3、4、5、6的点数，掷得面朝上的点数为奇数的概率为（ ）
| A． | $\frac{1}{6}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{2}$ |
8．已知P1（1，y1），P2（2，y2）是正比例函数y=x的图象上的两点，则y1，y2的大小关系为（ ）
| A． | y1=y2 | B． | y1＞y2 | ||
| C． | y1＜y2 | D． | y1，y2的大小关系不确定 |
12．在四边形ABCD中，对角线AC，BD互相平分，若添加一个条件使得四边形ABCD是矩形，则这个条件可以是（ ）
| A． | ∠ABC=90° | B． | AC⊥BD | C． | AB=CD | D． | AB∥CD |
如图，AB⊥BF，CD⊥BF，∠BAF=∠AFE，请说明∠ACD=∠E．
9．
如图，点O是菱形ABCD两边对角线的交点，过O点的三条直线将菱形分成阴影部分和空白部分．已知∠D=150°，AD=$\sqrt{5}$，则阴影部分的面积为（ ）
如图，点O是菱形ABCD两边对角线的交点，过O点的三条直线将菱形分成阴影部分和空白部分．已知∠D=150°，AD=$\sqrt{5}$，则阴影部分的面积为（ ）| A． | $\frac{1}{2}$$\sqrt{5}$ | B． | $\frac{5}{4}$ | C． | $\frac{1}{4}$$\sqrt{5}$ | D． | $\frac{3}{4}$ |
6．下列各式中是二次根式的是（ ）
| A． | $\sqrt{-7}$ | B． | $\root{4}{8}$ | C． | $\sqrt{{a}^{2}+1}$ | D． | $\root{3}{3}$ |
7．
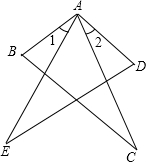如图，要用“SAS”证△ABC≌△ADE，若已知AB=AD，AC=AE，则需要条件是（ ）
如图，要用“SAS”证△ABC≌△ADE，若已知AB=AD，AC=AE，则需要条件是（ ）| A． | ∠1=∠2 | B． | ∠E=∠C | C． | ∠BAD=∠CAE | D． | ∠B=∠D |