题目内容
4.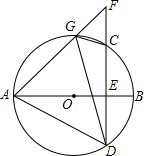 如图,AB是圆O的直径,弦CD⊥AB于点E,G是$\widehat{AC}$上任意一点,连结AD,GD,GC,延长AG、DC交于点F.
如图,AB是圆O的直径,弦CD⊥AB于点E,G是$\widehat{AC}$上任意一点,连结AD,GD,GC,延长AG、DC交于点F.(1)求证:∠FGC=∠AGD;
(2)若AD=GD,求证:△FCG为等腰三角形.
分析 (1)根据圆内接四边形的∠FGC=∠ADC,根据垂径定理得出$\widehat{AC}$=$\widehat{AD}$,推出∠AGD=∠ADC即可;
(2)根据圆内接四边形的∠FGC=∠ADC,∠FCG=∠GAD,求出∠FCG=∠FGC,根据等腰三角形的判定推出即可.
解答 证明:(1)∵A、D、C、G四点共圆,
∴∠FGC=∠ADC,
∵AB为直径,CD⊥AB,
∴$\widehat{AC}$=$\widehat{AD}$,
∴∠AGD=∠ADC,
∴∠FGC=∠AGD;
(2)∵A、D、C、G四点共圆,
∴∠FGC=∠ADC=∠AGD,∠FCG=∠GAD,
∵AD=GD,
∴∠GAD=∠DGA,
∴∠FCG=∠FGC,
∴FG=FC,
∴△FCG为等腰三角形.
点评 本题考查了垂径定理,圆内接四边形的性质,等腰三角形的性质和判定的应用,能综合运用定理进行推理是解此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,抛物线m:y=$\frac{1}{2}$x2平移得到抛物线n,抛物线m与x轴交于点O,点A.若它的顶点坐标为P(-3,-$\frac{9}{2}$),它的对称轴与抛物线y=$\frac{1}{2}$x2交于点O.
如图,抛物线m:y=$\frac{1}{2}$x2平移得到抛物线n,抛物线m与x轴交于点O,点A.若它的顶点坐标为P(-3,-$\frac{9}{2}$),它的对称轴与抛物线y=$\frac{1}{2}$x2交于点O.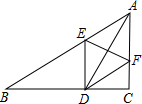 如图,△ABC中,∠C=90°,AD平分∠BAC,ED⊥BC,DF∥AB,求证:AD与EF互相垂直平分.
如图,△ABC中,∠C=90°,AD平分∠BAC,ED⊥BC,DF∥AB,求证:AD与EF互相垂直平分.