题目内容
12. 如图,在⊙O中,弦AB、DC的延长线交于点E,且DC=CE,C是$\widehat{BD}$的中点.求证:AD是⊙O的直径.
如图,在⊙O中,弦AB、DC的延长线交于点E,且DC=CE,C是$\widehat{BD}$的中点.求证:AD是⊙O的直径.
分析 先根据C是$\widehat{BD}$的中点得出DC=BC,再由DC=CE得出BC=CE,故∠E=∠EBC,由圆内接四边形的性质可得出∠EBC=∠D,故∠E=∠D,根据等腰三角形的性质即可得出结论.
解答 解:∵C是$\widehat{BD}$的中点,
∴DC=BC.
∵DC=CE,
∴BC=CE,
∴∠E=∠EBC.
∵四边形ABCD是圆内接四边形,
∴∠EBC=∠D,
∴∠E=∠D,
∴AE=AD.
∵DC=CE,
∴AD⊥DE,
∴∠ACD是直角,
∴AD是⊙O的直径.
点评 本题考查的是圆心角、弧、弦的关系,熟知在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等是解答此题的关键.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
2. 如图,点A的坐标为(-1,0),点B在第一、三象限的角平分线上运动,当线段AB最短时,点B的坐标为( )
如图,点A的坐标为(-1,0),点B在第一、三象限的角平分线上运动,当线段AB最短时,点B的坐标为( )
 如图,点A的坐标为(-1,0),点B在第一、三象限的角平分线上运动,当线段AB最短时,点B的坐标为( )
如图,点A的坐标为(-1,0),点B在第一、三象限的角平分线上运动,当线段AB最短时,点B的坐标为( )| A. | (0,0) | B. | ($\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$) | C. | (-$\frac{1}{2}$,-$\frac{1}{2}$) | D. | (-$\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$) |
3.已知a>b>c,设M=$\frac{2}{a-c}$,N=$\frac{1}{a-b}$-$\frac{1}{b-c}$,则M与N的大小关系为( )
| A. | M>N | B. | M=N | C. | M<N | D. | 无法确定 |
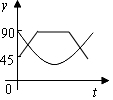
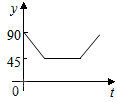
 如图,A、B、C、D为⊙O的四等分点,动点P从圆心O出发,沿O-C-D-O路线做匀速运动,设运动时间为t(秒),∠APB=y(度),则下列图象中表示y与t之间的函数关系最恰当的是( )
如图,A、B、C、D为⊙O的四等分点,动点P从圆心O出发,沿O-C-D-O路线做匀速运动,设运动时间为t(秒),∠APB=y(度),则下列图象中表示y与t之间的函数关系最恰当的是( )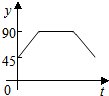

 如图,在三角形ABC中,AH是高,正方形DEFG的顶点D、G分别在AB、AC上,EF在BC上,设BC=120,AH=80,求正方形的边长.
如图,在三角形ABC中,AH是高,正方形DEFG的顶点D、G分别在AB、AC上,EF在BC上,设BC=120,AH=80,求正方形的边长. 如图,△ABC是⊙O的内接三角形,AB是⊙O的直径,OD⊥AB于点O,分别交AC、CF于点E、D,且CF是⊙O的切线.
如图,△ABC是⊙O的内接三角形,AB是⊙O的直径,OD⊥AB于点O,分别交AC、CF于点E、D,且CF是⊙O的切线. 如图,抛物线m:y=$\frac{1}{2}$x2平移得到抛物线n,抛物线m与x轴交于点O,点A.若它的顶点坐标为P(-3,-$\frac{9}{2}$),它的对称轴与抛物线y=$\frac{1}{2}$x2交于点O.
如图,抛物线m:y=$\frac{1}{2}$x2平移得到抛物线n,抛物线m与x轴交于点O,点A.若它的顶点坐标为P(-3,-$\frac{9}{2}$),它的对称轴与抛物线y=$\frac{1}{2}$x2交于点O.